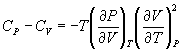
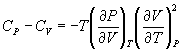
From the realtionships between specific heat and entropy, as given in Equn.3.3 and Equn.4.4,
→ (10.1)
→ (10.2)
Therefore,
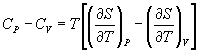→ (10.3)
Considering S as a function of T & V, as
differentiating,
→ (10.4)
Dividing Equn.10.4 by dT at constant P,
i.e.,
→ (10.5)
Therefore,
→ (10.6)
Cyclic relation rule: (for the function in the variables x, y & z)
→ (10.7)
We can write similar relation for the function in the variables P, T & V as
→ (10.8)
i.e.,
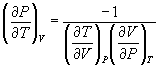→ (10.9)
and
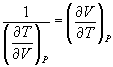→ (10.10)
Therefore,
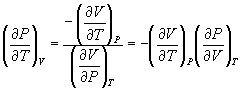→ (10.11)
Substituting for
from Equn.10.11 in Equn.10.6,
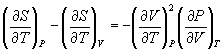→ (10.12)
Substituting from Equn.10.12, in Equn.10.3,
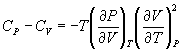→ (10.13)
Last Modified on: 01-May-2024
Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in