One mole of an ideal gas, initially at 20oC and 1 bar, undergoes the following mechanically reversible changes. It is compressed isothermally to a point such that when it is heated at constant volume to 100oC its final pressure is 10 bar. Calculate Q, W,
ΔU, and ΔH for the process. Take Cp = 7R/2 and Cv = 5R/2.Calculations:
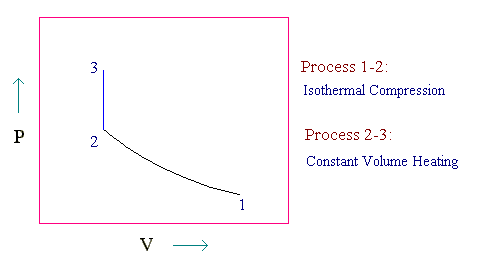
The given process is represented in PV diagram as follows:

We can find the pressure and volume of points 1, 2 and 3 by equation of state (ideal gas equation)
For one mole of ideal gas,
P1V1 = RT1
P2V2 = RT2
P3V3 = RT3
For the given process, T2 = T1 and V3 = V2.
V1 = R x (273 + 20)/1 = 293R
And V3 = R x (273 + 100) / 10 = 37.3R
For the point 2, P2 = R x (273 + 20) / (37.3R) = 293/37.3 = 7.855 bar
PVT conditions of the points 1,2 and 3's are:
|
Point |
P, bar |
V |
T, Kelvin |
|
1 |
1 |
293R |
293 |
|
2 |
7.855 |
37.3R |
293 |
|
3 |
10 |
37.3R |
373 |
For the isothermal process:
Δ
U = 0Δ
H = 0W = ∫PdV = ∫RT dV/V = RT ln (V2/V1) = R x 293 x ln (37.3/293) = -604R
Q = -W = 604R (since Q + W = ΔU)
Work is done on the system and heat is given out by the system
For the constant volume heating (isochoric process):
W = 0
Δ
U = Cv(T3 - T2) = (5R/2) x (373 - 293) = 200RΔ
H = Cp(T3 - T2) = (7R/2) x (373 - 293) = 280RQ = ΔU - W = 200R
Summary:
|
Process |
Q (heat given to the system) |
W (work done on the system) |
Δ U |
Δ H |
|
Isothermal compression |
-604R = -604 x 8.314 = -5021.66 J |
604R = 5021.66 J |
0 J |
0 J |
|
Constant volume heating |
200R = 1662.8 J |
0 J |
1662.8 J |
280R = 2327.92 J |
Last Modified on: 01-May-2024
Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in