In a mixture of quartz (sp.gr = 2.65) and galena (sp.gr = 7.5), the size of the particles range from 0.0002 cm to 0.001 cm. On separation in a hydraulic classifier using water under free settling conditions, what are the size ranges of quartz and galena in the pure products? (Viscosity of water = 0.001 kg/m.s; density = 1000 kg/m3).
Data:
Density of quartz(ρsa) = 2650 kg/m3
Density of galena(ρsb) = 7500 kg/m3
Particle size range(Dmin to Dmax): 0.0002 cm to 0.001 cm
Viscosity of water(μ) = 0.001 kg/m.sec
Density of water(ρ) = 1000 kg/m3
Formulae / Theory:
For laminar settling regimes, terminal-settling velocity is given by
Stokes law: (valid for NRe,p < 0.1)
ut = D2(ρs - ρ)g / (18μ)
where D is the diameter of particle
ρs is the density of solid
NRe,p = Dutρ/μ
For turbulent regime,
ut = [ 4D(ρs - ρ)g / (3CDρ)]0.5
CD is the drag coefficient.
If CD is assumed to be same for the two different density particles of the same diameter (assumption is valid in high turbulent velocities and practically assumed to be correct for laminar regime also),
for laminar flow, for equal settling velocities,
Da/Db = [ (ρsb - ρ) / (ρsa - ρ) ]0.5. → 1
Similarly for turbulent flow, for equal settling velocities,
Da/Db = [ (ρsb - ρ) / (ρsa - ρ) ].
Calculations:
First let us check for the flow regime for the given particle size range of particles:
For the largest diameter particle of higher density to follow laminar regime,
NRe,p = Dutρ/μ= D D2(ρs - ρ)g ρ /(18μ2) should be less than 0.1
i.e., the maximum size of particle is,
D3 = 0.1 x 18μ2/ (ρs - ρ)g ρ = 0.1 x 18 x 0.0012 / [(7500 - 1000) x 9.81 x 1000]
= 3.05 x 10-5 m = 0.00305 cm, which is well above the maximum size of the particles.
Therefore, laminar flow equations can be used for this problem.
The fractions obtained after separation are:
(i) Pure Galena only
(ii) Galena and quartz
(iii) Quartz only
The terminal settling velocity of minimum dia galena in fraction (i) corresponds to the settling velocity of maximum dia quartz particles.
From equn.1,
Da/Db = [ (ρsb - ρ) / (ρsa - ρ) ]0.5
Da/0.001 = [ (2.65 - 1)/(7.5 - 1) ]0.5
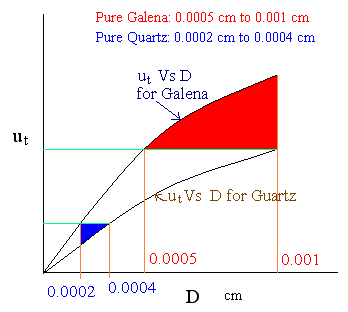
Da = 0.0005 cm
The fraction (i) consists of pure galena in the size range 0.0005 cm to 0.001 cm
The terminal settling velocity of maximum dia quartz in fraction (ii) corresponds to the settling velocity of minimum dia galena particles.
From equn.1,
Da/0.0002 = [ (7.5 - 1)/(2.65 - 1) ]0.5
Da = 0.0004 cm
The fraction (iii) consists of pure quartz in the size range 0.0002 cm to 0.0004 cm
The fraction (ii) consists of quartz in the size range 0.0004 cm to 0.001 cm, and galena in the size range 0.0002 cm to 0.0005 cm.
This result is shown in the following diagram.

Last Modified on: 30-Apr-2024
Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in