Heat Exchanger Area Comparison for Parallel and Counter Flow

Home -> ChE Learning Resources -> Solved Problems -> Heat Transfer->

A heat exchanger heats 25,000 kg/hr of water entering at 30oC while cooling 20,000 kg/hr of water from 100oC to 80oC. Determine the area necessary for (i) Parallel flow arrangement
(ii) Counter flow arrangement.
Overall heat transfer coefficient may be assumed as 1,600 W/m2K.

Calculations:

Heat of heat transferred by the cooling water = Q = mCpΔT = 20000 x 4.184 x (100 - 80) = 1673600 kJ/hr = 464.89 kW

This will be the amount of heat transferred to the water that is getting heated up. Therefore, temperature change is = 1673600 / (25000 x 4.184) = 16oC

i.e., outlet temperature = 30 + 16 = 46oC

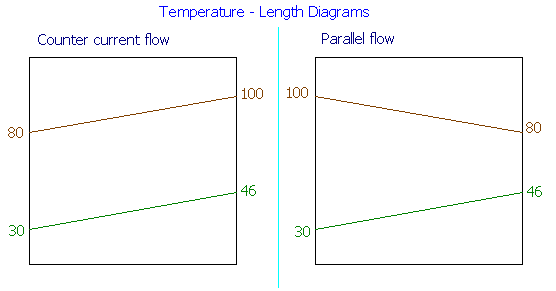
With these data, the following temperature-length diagram is drawn.

temperature profile of cocurrent and countercurrent

(i) Parallel flow arrangement:

ΔTo = 100 - 30 = 70oC

ΔTL = 80 - 46 = 34oC

LMTD = ΔTln = (ΔTo - ΔTL) / ln (ΔTo/ΔTL)

= (70 - 34) / ln (70/34) = 49.85oC

A = Q / (UΔTln) = 464.89 x 103 / (1600 x 49.85) = 5.8286 m2

Area required for parallel flow = 5.8286 m2

(ii) Counter flow arrangement:

ΔTo = 80 - 30 = 50oC

ΔTL = 100 - 46 = 54oC

LMTD = ΔTln = (ΔTo - ΔTL) / ln (ΔTo/ΔTL)

= (50 - 54) / ln (50/54) = 51.97oC

A = Q / (UΔTln) = 464.89 x 103 / (1600 x 51.97) = 5.5908 m2

Area required for counter flow = 5.5908 m2
[Index]

Last Modified on: 01-May-2024

Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in