A steel sphere is of inner diameter 40 cm and outer diameter 45 cm is used to store liquid oxygen (B.P is minus 183oC). The sphere is covered with one layer of insulation, of thickness 50 mm whose K is 0.35 W/m.K and another insulation, of thickness 50 mm whose K is 0.098 W/m.K. The sphere is exposed to atmosphere of 25oC. Find out the rate of oxygen becoming vapor every minute. Latent heat of oxygen is 370 kJ/kg. Thermal conductivity of steel = 20 W/m.K. Heat transfer coefficient of ambient air = 80 W/m2.K
Calculations:
For composite concentric sphere, the rate of heat transfer from outside to the sphere Q, is given by,
Q = (Ta - Tb)/R
Ta = 25oC
Tb = -183oC
Where, R = Rs + Rins,1 + Rins,2 + Ra
Ra = air film resistance = 1 / (4πra2ha)
Rins,2 = Resistance offered by the outer insulation = (ra - r1) / (4πkins,2rar1)
Rins,1 = Resistance offered by the inner insulation = (r1 - r2) / (4πkins,1r1r2)
Rs = Resistance offered by the metal wall (steel) = (r2 - rb) / (4πksr2rb)
Given Data:
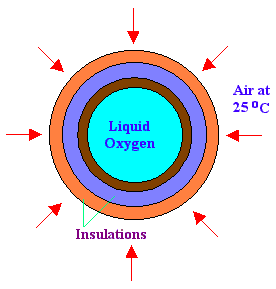
Diameter of sphere with insulation = 45 + 2 x 5 + 2 x 5 = 65 cm
ra = 32.5 cm = 0.325 m
r1 = 32.5 - 5 = 27.5 cm = 0.275 m
r2 = 27.5 - 5 = 22.5 cm = 0.225 m
rb = 20 cm = 0.2 m
Substituting these data in the above equations,
Ra = 1/(4 x 3.142 x 0.3252 x 80) = 9.4175 x 10-3 oC/W
Rins,2 = (0.325 - 0.275)/(4 x 3.142 x 0.098 x 0.325 x 0.275) = 0.4543 oC/W
Rins,1 = (0.275 - 0.225)/(4 x 3.142 x 0.35 x 0.275 x 0.225) = 0.1837 oC/W
Rs = (0.225 - 0.2)/(4 x 3.142 x 20 x 0.225 x 0.2) = 2.2105 x 10-3 oC/W
R = 9.4175 x 10-3 + 0.4543 + 0.1837 + 2.2105 x 10-3 = 0.6496 oC/W
Q = (25 + 183)/0.6496 = 320.2 W
Rate of heat in per second = 320.2 J
Rate of heat in per minute = 320.2 x 60 = 19212 J = 19.212 kJ
370 kJ of heat is needed to vaporize 1 kg of liquid oxygen. Therefore, for the heat input of 19.212 kJ/min,
rate of oxygen becoming vapor = 19.212/370 = 0.0519 kg/min
Last Modified on: 01-May-2024
Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in