Length of Heat Exchanger

Home -> ChE Learning Resources -> Solved Problems -> Heat Transfer->

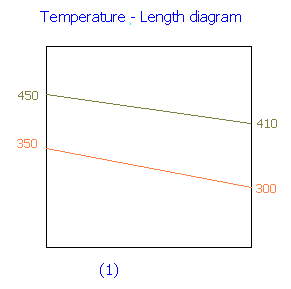
In a counter-current heat exchanger, an oil stream is cooled from 450 K to 410 K by water inlet and outlet temperatures of 300 K and 350 K respectively. The exchanger consists a number of tubes of 1 m length each. It is now desired to cool the oil to 390 K (instead of 410 K) while maintaining the flow rate of oil, flow rate of water, inlet temperature of oil and water, and the number of tubes at the same values as before. Calculate the length of each tube required for this purpose. Assume that the physical properties remain unchanged.

Calculations:

For the first case:

temperature profile counter-current heat exchanger

ΔTln,1 = LMTD = (ΔTo - ΔTL) / ln (ΔTo/ΔTL)

ΔTo = 450 - 350 = 100 K

ΔTL = 410 - 300 = 110 K

ΔTln,1 = (100 - 110) / ln (100/110) = 104.9 K

For the second case:

Outlet temperature of water is obtained from the following proportionality factor.

For 40 K change in oil temperature, there is a change of 50 K in water temperature. Since the flow rates are not changed, for a change of 60 K (i.e., = [ 450 - 390] K) in oil temperature the corresponding change in water temperature = 60 x 50 / 40 = 75 K

Therefore, outlet temperature of water = 300 + 75 = 375 K

And heat transfer rate for the second case will be 50% more than that of the first case, since there is a 50% increase in temperature drop.

i.e.,

Q2 = 1.5 Q1

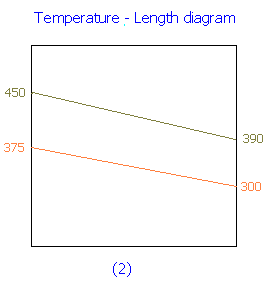
temperature profile counter-current heat exchanger

ΔTo = 450 - 375 = 75 K

ΔTL = 390 - 300 = 90 K

ΔTln,2 = (75 - 90) / ln (75/90) = 82.3 K

Since there is no change in physical properties of fluid compared to the first case, overall heat transfer coefficient U will be the same for both the cases.

Heat transfer rate Q = U A ΔTln

and

A = n π D L

i.e., 'A' is directly proportional to 'L'

For a given diameter and number of tubes it can be written as,

Q = C L ΔTln

where C is a constant.

For the first case,

Q1 = C L1 ΔTln,1

Q1 = C x 1 x 104.9

Q1/C = 104.9 → 1

For the second case,

Q2 = C L2 ΔTln,2

Since Q2 = 1.5 Q1,

the above equation can be written as,

1.5 Q1 = C L2 ΔTln,2

L2 = 1.5 (Q1/C) (1/ΔTln,2) → 2

Substituting for Q1/C from Equn.1 in Equn.2,

L2 = 1.5 x 104.9 / 82.3 = 1.912 m

Length of each tube required for the second case = 1.912 m  
[Index]

Last Modified on: 01-May-2024

Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in