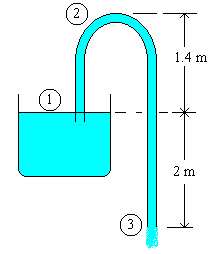
A siphon consisting of a 3 cm diameter tube is used to drain water from a tank. The outlet end of the tube is 2 m below the water surface in the tank. Neglecting friction, calculate the discharge. If the peak point of the siphon is 1.4 m above the water surface in the tank, estimate the pressure of fluid at the point of siphon.
Data:
Dia of tube = 3 cm = 0.03 m

Formula:
Bernoulli's equation for frictionless flow is
\(\displaystyle \frac{p}{\rho g} + \frac{v^2}{2g} + z = \text{ constant} \)
Discharge (Q) = cross sectional area x velocity
Calculations:
Applying Bernoulli's equation for the points 1 and 3, ( i.e. comparing the energy levels for the fluid in the tank surface and at the discharge point of tube)
p1 = 0 N/m2(g)
p3 = 0 N/m2(g)
z1 = 0 m
z3 = -2 m
Since the rate of fall of liquid level in the tank is almost negligible,
v1 = 0 m/sec.
Therefore,
0 + 0 + 0 = 0 + (v32 / 2g) - 2
v3 = (2 x 2g)0.5 = 6.265 m/sec
Q = (π/4)D2 v = (π/4) x 0.032 x 6.265 = 0.00443 m3/sec = 15.94 m3/hr
Applying Bernoulli's equation for the points 1 and 2, ( i.e. comparing the energy levels for the fluid at the tank surface to the peak point of siphon)
p1 = 0 N/m2(g)
z2 = 1.4 m
v2 = v3 = 6.265 m/sec (since the cross sectional area of sections 2 and 3 are the same)
0 + 0 + 0 = p2 / (
ρg) + 6.2652 / (2g) + 1.4p2 / (
ρg) = -3.4 mp2 = -3.4 x 1000 x 9.812 N/m2(g) = -33360.8 N/m2(g)
Absolute pressure at point 2 = 101325 - 33360.8 =
67964.2 N/m2(a)Last Modified on: 01-May-2024
Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in