Flow in Siphon

Home -> ChE Learning Resources -> Solved Problems -> Fluid Mechanics->

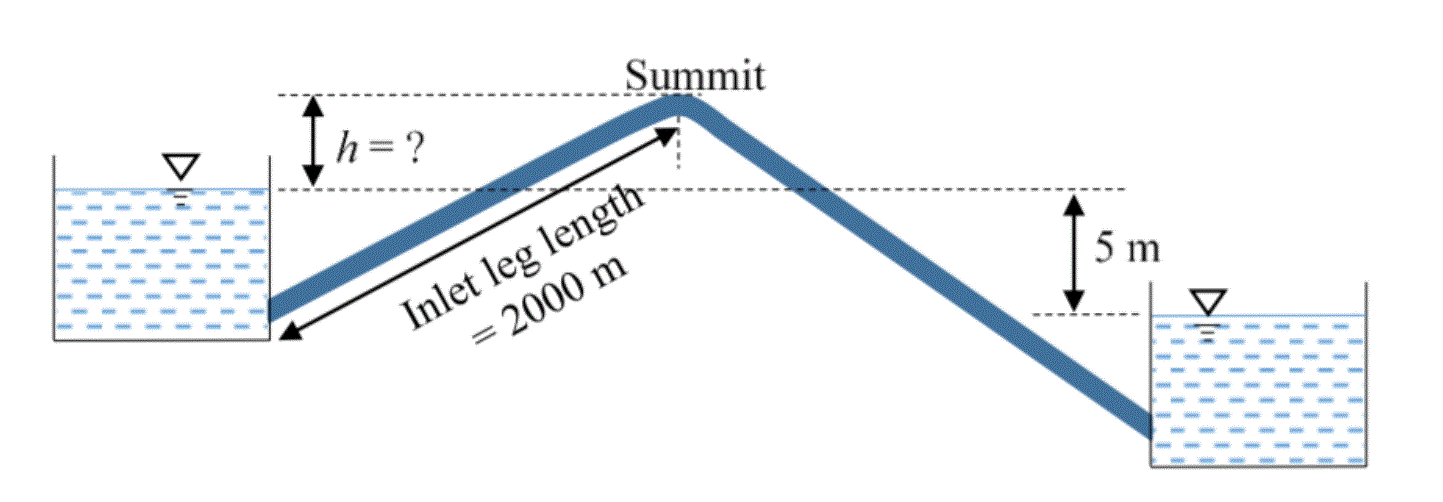
Siphon Connecting Two Reservoirs

Two water reservoirs are connected by a siphon (running full) of total length 5000 m and diameter of 0.10 m, as shown below (figure not drawn to scale).

Siphon Connecting Two Open Reservoirs

The inlet leg length of the siphon to its summit is 2000 m. The difference in the water surface levels of the two reservoirs is 5 m. Assume the permissible minimum absolute pressure at the summit of the siphon to be 2.5 m of water when running full. Given: Darcy friction factor = 0.02 throughout, atmospheric pressure = 10.3 m of water, and acceleration due to gravity \(g=9.81\) m/s2. Considering only major loss using Darcy-Weisbach equation, the maximum height of the summit of siphon from the water level of upper reservoir, \(h\) (in m, round off to 1 decimal place) is __________ 

 (GATE-CE-20219-S1-50)

Solution:

Find velocity of fluid by equating head-difference between two reservoirs to losses due to friction.

i.e., 5 m = losses due to friction

\[  h_f = \frac{\Delta P}{\rho g} = \frac{2fL\rho v^2}{D\rho g} = \frac{2fL v^2}{D g} \]

Given: \( f_D = 0.02\). We know, \(f_D = 4f\). Therefore, \(f = 0.02/4 = 0.005\)

\[  5 = \frac{2\times0.005\times5000\times v^2}{0.1\times9.81}  \qquad \Longrightarrow \quad v = 0.313 \text{ m/s}\]

For the summit height:

Making energy balance (in terms of m of water column, between top reservoir's level and summit:

\[ 10.3 - h_f = 2.5 + h \]

where

\[ h_f = \frac{2fL v^2}{D g} = \frac{2\times0.005\times2000\times0.313^2}{0.1\times9.81} = 2 \text{ m} \]

Therefore,

\[ h = 10.3 - 2 - 2.5 = 5.8 \text{ m} \]

[Index]

Last Modified on: 01-May-2024

Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in