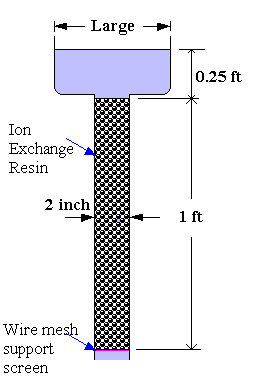
Figure shows a water softener in which water trickles by gravity over a bed of spherical ion-exchange resin particles, each 0.05 inch in diameter. The bed has a porosity of 0.33. Calculate the volumetric flow rate of water.

Calculations:
Data:
μ = 1 cp = 1 x 6.72x10-4 lb/(ft.sec)
ε = 0.33
ρ = 62.3 lb/ft3
ΔL = 1 ft
g = 32.2 ft/sec2
Formula:
Applying Bernoulli's equation from the top surface of the fluid to the outlet of the packed bed and ignoring the kinetic-energy term and the pressure drop through the support screen, which are both small, we find
g(ΔL) = hf
hf = Δp/ρ
For laminar flow, (Blake-Kozeny Equation)
\(\displaystyle \frac{\Delta p}{\rho} = 150\frac{V_s\mu(1-\varepsilon)^2\Delta L}{D_p^2\varepsilon^3\rho} \)
Calculations:
Therefore, Vs = 32.2 x 1.25 x (0.05/12)2 x 0.333 x 62.3 / ( 150 x (1 x 6.72x10-4) x (1 - 0.33)2 x 1)
= 0.035 ft/sec = 0.011 m/sec.
Q = AVs = (2/12)2 x (π/4) x 0.035 = 0.00075 ft3/sec = 21 cm3/sec
Before accepting this as the correct solution, we check the NRepm.
NRepm= (0.05/12) x 0.035 x 62.3 / (1 x 6.72x10-4 x (1 - 0.33) ) = 20.2
This is slightly above the value of 10 (up to which the Blake-Kozeny Equation can be used), for which we can safely use without appreciable error.
Last Modified on: 01-May-2024
Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in