Fluid Mechanics - Class Test Questions

Home -> ChE Learning Resources -> Question Bank

4HE - Fluid Mechanics

Test - 1 (22-Jan-2001)        Maximum Marks : 60         Duration : 90 min

    Part A (12 x 2 = 24 Marks)

  1. What is a Newtonian fluid? Give two examples.

    Fluid which obeys the Newton's law of viscosity:

    t = m du/dy are said to be Newtonian fluids.

    Examples: water, air, kerosene.

  2. Give suitable examples for (a) Bingham plastic fluid, (b) Thixotropic fluid

    (a) Bingham plastic fluid: Tooth paste, gels, sewage sludge

    (b) Thixotropic fluid: paint

  3. The viscosity of an oil is 10 cP. Reexpress in both lb, ft, sec system and in S.I. units.

    lb-ft-sec units: 10 cP = 10 x 10-3 kg/m.sec = 0.01 x 2.203/(3.281 x 1) lb/ft.sec = 6.713 lb/ft.sec

    S.I: 10 cP = 0.01 kg/m.sec

  4. Define 'Bulk modulus'. Write down its units.

    Bulk modulus (K) = (change in pressure) / (volumetric strain)

    Volumetric strain is the change in volume divided by the original volume. Therefore,
    (change in volume) / (original volume) = (change in pressure) / (bulk modulus)

    i.e., -dV/V = dp/K Negative sign for dV indicates the volume decreases as pressure increases.

    In the limit, as dp tends to 0,

    K = -V dp/dV

    In terms of density, K = rdp/dr

    Bulk modulus has the units of pressure; N/m2.

  5. Calculate the approximate depression of mercury at 20oC in a capillary tube of radius 1.5 mm
    6. s = 0.514 N/m, r = 13.6 g/cc, q = 140o

    h = 4scos(q)/(rgd)

    h = 4 x 0.514 x cos(140)/(13.6 x 1000 x 9.812 x 3 x 10-3)

    i.e., h = 3.93 mm

  6. State the Pascal's law of pressure at a point in a fluid.

    Pressure at a point is same in all directions. This is Pascal's law. This applies to fluid at rest

  7. It is impossible to have gauge pressures that are as low as -20 psig. Justify this statement.

    -20 psig = -20 + 14.7 = -5.3 psia. The minimum possible pressure is only 0 psia. Therefore, the given gauge pressure is an impossible one.

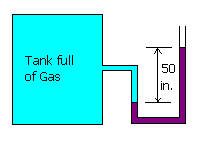  8. The fluid in the manometer (shown in figure) is ethyl iodide with sp.gr = 1.93. The manometeric fluid height difference is 50 in. What is the gauge pressure in the tank? What is the absolute pressure in the tank?

    DP = rgh = 1.93 x 1000 x 9.812 x 50 x 0.0254 = 24.05 kN/m2(g) = (101.3 + 24.05) kN/m2(a) = 125.35 kN/m2(a)

  9. Differentiate between 'steady' and 'unsteady flow' with suitable examples.

  10. Define 'ideal fluid'. What is the value of Reynolds number for an ideal fluid?

    Ideal fluid is a hypothetical fluid which is assumed to have a viscoisty of zero, and incompressible.

    Reynolds number of an ideal fluid is infinity.

  11. (a) Determine whether the velocity components given below satisfy the equation of continuity:

    12. u = 2x2 + zy
    v = -2xy + 3y2 + 3zy
    w = -1.5z2 - 2xz - 6yz.
    where u, v and w are velocity components in x, y and z directions respectively.

    u/x = 4x
    v/y = -2x + 6y + 3z
    w/z = -3z - 2x - 6y

    u/x + v/y + w/z = 0.

    Therefore, continuity equation is satisfied.

  12. Write Bernoulli's equation. State its assumptions.

    Flow is steady, inviscid and incompressible.

    There are no addition of energy in between the the sections considered.

    Part B (3 x 12 = 36 Marks)

  13. Derive expressions for the variation of pressure with altitude (i) for adiabatic atmosphere
    (ii) for the atmosphere in which the temperature decreases with altitude at a constant rate.

    (i) Variation of pressure with distance is given by,

    dp/dz = -rg           --> 1

    For adiabatic atmosphere, pVg = constant

    i.e.,       p/rg = constant

    p/rg = p1/r1g

    r = r1(p/p1)g = B pg     --> 2
    where B is a constant = r1/p1g

    Substituting from equn.2 in equn.1,

    dp/dz = -B pgg

    Separating the varaiables and integrating,

    -dp/pg = Bg dz

    [1/(g - 1)] p-g+1 = Bgz + C

    where C is a constant.

    The constant C can be eliminated by substituting the initial conditions; that when z = z1, p = p1

    C = [1/(g - 1)] p1-g+1 - Bgz1

    Therefore, [1/(g - 1)] p-g+1 = Bgz + [1/(g - 1)] p1-g+1 - Bgz1

    (ii) For the atmosphere in which the temperature decreases with height at a constant rate, T = To - Cz
    where To is the temperature at the ground level; and C is the rate of change of temperature with height(z).

    dp/dz = -rg = -(pM/RT)g = -pM/[R(To + Cz)]
    where M is the molecular weight of air.

    Separating the variables,

    dp/p = -M/[R(To + Cz)] dz

    ln p = -M/(RC) ln (To + Cz) + D
    where D is a constant;

    The constant D can be eliminated from the substitution of initial conditions, p = p1 when z = z1

    D = ln p1 + M/(RC) ln (To + Cz1)

    Therefore, ln p/p1 = M/(RC) ln [(To + Cz1)/(To + Cz)]

    Or

  14. On a very cold day at the New Delhi, the temperature of air is 5oC. Assuming that the air remains isothermal up to a 10,000 ft elevation and that the pressure at the sea level is 1 atm, calculate the pressure at 10,000 ft.

    15. Variation of pressure with distance is given by,

    dp/dz = -rg           --> 1

    Assuming that air is following ideal gas relationship, r-5 p.

    Substituting for r in Equn.1, dp/p = -1.255 x 10-5 x 9.812 dz Integrating between the limits: (z1 = 0, p1 = 1 atm = 1.01325 x 105 N/m2; and when z2 = 10,000 ft = 3048 m, p2 = ?)

    ln (p2/p1) = -1.255 x 10-5 x 9.812 x (z2 - z1)

    i.e.,

    p2/1.01325 x 105 = e-0.3753 = 0.687

    Therefore, p2 = 0.6962 x 105 N/m2 = 0.687 atm (a).

  15. (i) Derive an expression for the pressure difference across two limbs of an 'Inclined U-tube manomater' with one leg of enlarged diamater, interms of the measurable quantities.
    (ii) What is the error if the movement of the fluid in the larger dia leg is ignored?
    (iii) What factors influence the sensitivity of manometer?

    Or

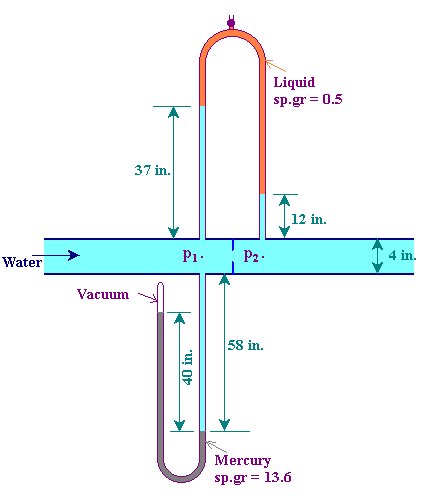  16. A closed-U-tube manometer filled with mercury is attached to the underside of a line carrying water, as shown in figure. At a point directly above the closed-U-tube manometer tap, the upstream tap of an inverted U tube is located. The inverted-U-tube manometer is filled with a liquid of specific gravity 0.5. What are p1 and p2 in psia?

    Balance for the mercury manometer:

    40 x 13.6 = p1 + (58 + 2) x 1 p1 = 40 x 13.6 - 60 inch water = 12.294 m water = 17.485 psia

    Balance for the inverted manometer:

    p1 - 39 x 1 = p2 - 14 x 1 - 25 x 0.5

    p1 - p2 = 25 x 1 - 25 x 0.5 = 12.5 inch water = 0.3175 m water = 0.03074 atm = 0.452 psi.

    Therefore, p2 = 17.485 - 0.452 = 17.006 psia.

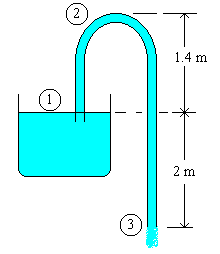
  17. A siphon consisting of a 3 cm diameter tube is used to drain water from a tank. The outlet end of the tube is 2 m below the water surface in the tank. Water is at 25oC. (i) Neglecting friction, calculate the discharge.
    (ii) If the peak point of the siphon is 1.4 m above the water surface in the tank, estimate the pressure of fluid at the point of siphon.
    (iii) Estimate the maximum distance between water surface and the peak point of siphon, so that the flow is not getting disturbed.     (vapor pressure of water at 25oC = 316.6 N/m2)

    The given problem is shown as a diagram:

    Bernoulli's equation for frictionless flow is:

    (a) Applying Bernoulli's equation for the points 1 and 3, ( i.e. comparing the energy levels for the fluid in the tank surface and at the discharge point of tube)

    p1 = 0 N/m2(g)

    p3 = 0 N/m2(g)

    z1 = 0 m

    z3 = -2 m

    Since the rate of fall of liquid level in the tank is almost negligible,

    v1 = 0 m/sec.

    Therefore,

    0 + 0 + 0 = 0 + (v32 / 2g) - 2

    v3 = (2 x 2g)0.5 = 6.265 m/sec

    Discharge Q = (p/4)D2 v = (p/4) x 0.032 x 6.265 = 0.00443 m3/sec = 15.94 m3/hr

    (b) Applying Bernoulli's equation for the points 1 and 2, ( i.e. comparing the energy levels for the fluid at the tank surface to the peak point of siphon)

    p1 = 0 N/m2(g)

    z2 = 1.4 m

    v2 = v3 = 6.265 m/sec (since the cross sectional area of sections 2 and 3 are the same)

    0 + 0 + 0 = p2 / (rg) + 6.2652 / (2g) + 1.4

    p2 / (rg) = -3.4 m

    p2 = -3.4 x 1000 x 9.812 N/m2(g) = -33360.8 N/m2(g)

    Absolute pressure at point 2 = 101325 - 33360.8 = 67964.2 N/m2(a)

    (c) Maximum height is obtained by setting p2 = 316.6 N/m2(a):

    Applying Bernoulli's equation between points 1 and 2,

    1.01325 x 105/(1000 x 9.812) + 0 + 0 = 316.6/(1000 x 9.812) + 6.2652/(2g) + hmax

    Therefore, hmax = 8.294 meter

    Or

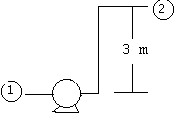  18. The following data were obtained on a section of piping through which an incompressible viscous fluid is flowing ( See Figure)

    Point 1:

    Pressure = 1.25 x 105 Pa
    Cross-sectional area = 15 x 10-4 m2
    Fluid Velocity = 1 m/s

    Point 2:

    Pressure = 1.05 x 105 Pa
    Cross-sectional area = 5 x 10-4 m2
    Elevation above point 1 = 3 m

    Other Data:

    Density of fluid = 1000 kg/m3
    Power delivered by the pump = 7.5 W
    assume efficiency = 100%)

    Predict whether flow is taking place from point 1 to 2 or from 2 to 1.

    By equation of continuity,

    A1v1 = A2v2

    Therefore, v2 = 15 x 1 / 5 = 3 m/sec.

    Mass flow rate = r Q = 1000 x 15 x 10-4 x 1 = 1.5 kg/sec.

    Pump head = 7.5 / (1.5 x 9.812) = 0.51 m

    Assuming flow is from 1 to 2, we can write the Bernoulli equation between 1 and 2 as,

    where 'q' is the work done by pump and 'w' is the work done by the fluid, and h is the head loss by friction.

    Substituting for the known quantites, 1.25 x 105/(1000 x 9.812) + 12/(2 x 9.812) = 1.05 x 105/(1000 x 9.812) + 32/(2 x 9.812) + 3 + h + 0 - 0.51

    12.74 + 0.051 + 0 = 10.7 + 0.459 + 3 + h - 0.51

    Therefore, h = -0.858 m.

    For a possible flow, h can not be negative. Therefore, the assumed direction is not correct.

    Let us rework for flow from 2 to 1:

    Then,

    1.05 x 105/(1000 x 9.812) + 32/(2 x 9.812) + 3 = 1.25 x 105/(1000 x 9.812) + 12/(2 x 9.812) + h + 0 - 0.51

    10.7 + 0.459 + 3 = 12.74 + 0.051 + 0 + h - 0.51

    Therefore, h = 1.419 m, which is a positive quantity; therefore, flow is from 2 to 1.

[Index]     [ Get More Questions with Solutions from Our Online Course...]

Last Modified on: 04-Feb-2022

Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in