Fluid Flow through Packed Bed

Home -> Lecture Notes -> Fluid Mechanics -> Unit-IV

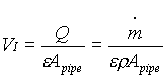
Consider a porous medium consisting of sand or some porous rock or glass beads or cotton cloth contained in a pipe. At any one cross section perpendicular to the flow, the average velocity may be based on the entire cross sectional area of pipe, in which case it is called the superficial velocity V_s

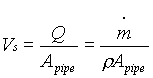
Or it may be based on the area actually open to the flowing fluid, in which case it is called the interstitial velocity V_I

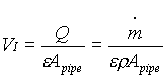
Where e is the porosity or void fraction.

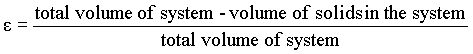
Previously it was indicated that for non-circular ducts, the friction factor plot could be used if we replaced the diameter in both the friction factor and the Reynolds number with 4 times the hydraulic radius (r_H)

The hydraulic radius (r_H) is the cross sectional area perpendicular to flow divided by the wetted perimeter. For a uniform duct this is a constant. For a packed bed it varies from point to point. But if we multiply both the cross sectional area and the perimeter by the length of the bed, it becomes,

r_H for porous medium = volume open to flow / total wetted surface

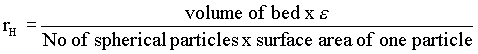
i.e.

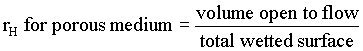
 But,

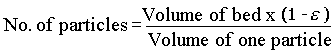
Therefore,

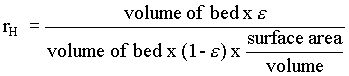
i.e.

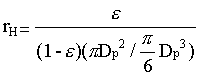
i.e.

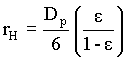
h_f = Dp / r = 2fLV_I² / D_e

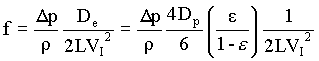
substituting for V_I in terms of V_S

i.e. V_I = V_S / e

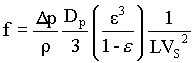
NRe = D_e V_I r / m

Substituting for D_e and V_I

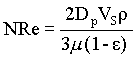
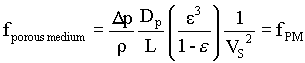
As in the case of flow in pipes, there are several different friction factors in common usage for flowing in porous media, all differing by a constant.

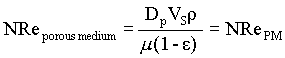
i.e. f_PM = 3f

and NRe_PM = 3NRe / 2

 For laminar flow, f = 16 / NRe

Therefore,

f_PM / 3 = 16 / (2NRe_PM / 3)

f_PM = 72 / NRe_PM

There is one obvious error in this derivation, namely the tacit assumption that the flow is in the x direction.

Actually, the flow is zigzag; it must pass around one particle and then through another. If we assume that this zigzag proceeds with an average angle 45^o to the x axis, then the actual flow path is Ö 2 times as long as the flow path, and the actual interstitial velocity is Ö 2 times the interstitial velocity used in the above equation. If we make these changes, we conclude that to agree with the friction factor plot, laminar flow in a porous medium made of uniformly sized spheres should be described by f_PM = 144 / NRe_PM

Experimental data indicate that the constant is about 150, so that for laminar flow we find experimentally,

f_{PM =} 150 / NRe_PM

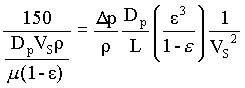
i.e.

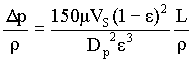
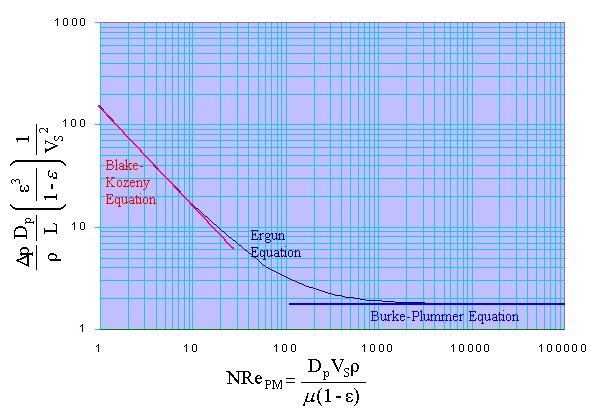
This equation is called as Blake-Kozeny equation or as Kozeny-Carman equation. It is valid for NRe_PM less than about 10.

Turbulent flow:

f_PM = 1.75 (experimental value)

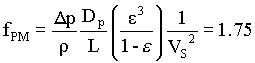
Therefore,

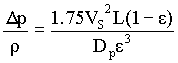
This is the Burke-Plummer equation, valid for NRe_PM greater than 1000

Since there is a smooth transition from all-laminar to all-turbulent flow, Ergun showed that if we add the friction factor term,

f_PM = 1.75 + 150 / NRe_PM

the transition regions data are predicted reasonably well.

i.e.

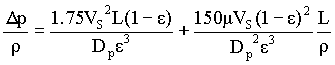
This is the Ergun's equation.

For non-spherical particles instead of diameter an equivalent diameter is defined.

The equivalent diameter of a non-spherical particle is defined as a sphere having the same volume as the particle. Sphericity is the ratio of surface area of this sphere to the actual surface area of particle.

The formula for sphericity is reduced to

Sphericity (F_s) = 6v_p/ (D_pS_p)

Where v_p is the volume of particle, D_p is the characteristic dimension of particle, and S_p is the surface area of particle.

For non-spherical particle Ergun equation is given by,