Drag Force on Solid Particles in Fluids

Home -> Lecture Notes -> Fluid Mechanics -> Unit-IV

Force in the direction of flow exerted by the fluid on the solid is called drag.

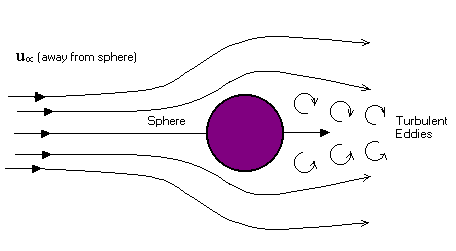
Figure shows a stationary smooth sphere of diameter D_P situated in a stream, whose velocity far away from the sphere is uµ to the right. Except at very low velocities, when the flow is entirely laminar, the wake immediately downstream from the sphere is unstable, and turbulent vortices will constantly be shed from various locations round the sphere. Because of turbulence, the pressure on the downstream side of the sphere will never fully recovered to that on the upstream side, and there will be a form drag to the right of the sphere. (For purely laminar flow, the pressure recovery is complete, and the form drag is zero.)

In addition, because of the velocity gradients that exist near the sphere, there will also be a net viscous drag (also called as wall drag) to the right (In potential flow there is no wall drag). The sum of these two effects is known as the (total) drag force, F_D. A similar drag occurs for spheres and other objects moving through an otherwise stationary fluid - it is the relative velocity that counts.

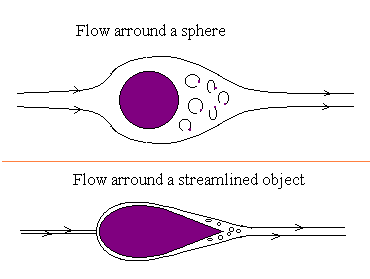
Form drag can be minimized by forcing separations toward the rear of the body. This is accomplished by stream lining. (see figure)

The experimental results of the drag on a smooth sphere may be correlated in terms of two dimensionless groups - the drag coefficient C_D and particles Reynolds number NRe_P:

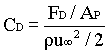
NRe_P = ru_µ D_P/m

In which A_P = pD_P²/4 is the projected area of the sphere in the direction of motion, and r and m are the properties of the fluid.

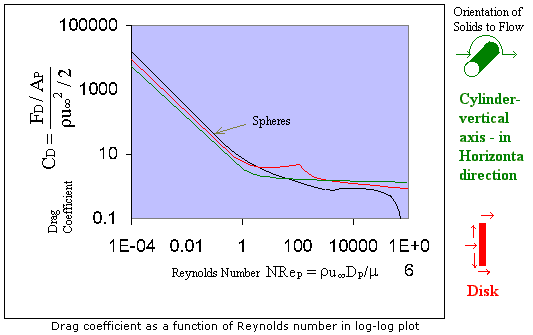
There are at least three distinct regions, for flow around a sphere.

1. For NRe_P less than 1 (laminar), C_D vs. NRe_P is a straight line, and is given by the relation

C_D = 24/NRe_P (given by Stoke's law, F_D = 3pm u_µ D_P)

2. 1 < NRe_P < 1000 , C_D = 18 NRe_P^-0.6 (transition)
3. 1000 < NRe_P < 2 x 10⁵ , C_D = 0.44 (turbulent)

For cylinders and disks, for NRe_P up to 1, C_D = 24/NRe and in other regimes C_D varies with NRe_P in the manner as shown in figure. Here the flow orientation is much important. Drag coefficients varies with orientation of solid to the flow direction.

In all these curves the transition from laminar to turbulent flow is more gradual than that for pipe flow (f vs. NRe curve).