The venturi meter described earlier is a reliable flow measuring device. Furthermore, it causes little pressure loss. For these reasons it is widely used, particularly for large-volume liquid and gas flows. However this meter is relatively complex to construct and hence expensive. Especially for small pipelines, its cost seems prohibitive, so simpler devices such as orifice meters are used.

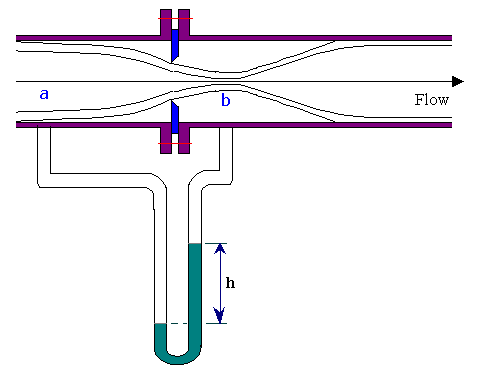
The orifice meter consists of a flat orifice plate with a circular hole drilled in it. There is a pressure tap upstream from the orifice plate and another just downstream. There are three recognized methods of placing the taps. And the coefficient of the meter will depend upon the position of taps.
|
Type of tap |
Distance of upstream tap from face of orifice |
Distance of downstream tap from downstream face |
|
Flange |
1 inch |
1 inch |
|
Vena contracta |
1 pipe diameter (actual inside) |
0.3 to 0.8 pipe diameter, depending on b |
|
Pipe |
2.5 times nominal pipe diameter |
8 times nominal pipe diameter |
The principle of the orifice meter is identical with that of the venturi meter. The reduction of the cross section of the flowing stream in passing through the orifice increases the velocity head at the expense of the pressure head, and the reduction in pressure between the taps is measured by a manometer. Bernoulli's equation provides a basis for correlating the increase in velocity head with the decrease in pressure head.
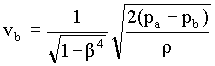 à 1
à 1
where b = Db/Da = (Ab/Aa)0.5
One important complication appears in the orifice meter that is not found in the venturi. The area of flow decreases from Aa at section 'a' to cross section of orifice opening (Ao) at the orifice and then to Ab at the vena contracta. The area at the vena contracta can be conveniently related to the area of the orifice by the coefficient of contraction Cc defined by the relation:
Cc = Ab / Ao
Therefore, vbAb = voAo , i.e., vo = vbCc
Inserting the value of Ab = CcAo in equn.1
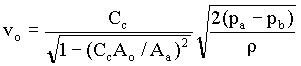
using the coefficient of discharge Co (orifice coefficient) to take the account of frictional losses in the meter and the parameter Cc, the flow rate (Q) through the pipe is obtained as,
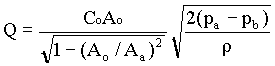
Co varies considerably with changes in Ao/Aa ratio and Reynolds number. A orifice coefficient (Co) of 0.61 may be taken for the standard meter for Reynolds numbers in excess of 104, though the value changes noticeably at lower values of Reynolds number.
Orifice pressure recovery:
Permanent pressure loss depends on the value of b. (b = Do/Da). For a value of b = 0.5, the lost head is about 73% of the orifice differential.
Last Modified on: 14-Sep-2014
Chemical Engineering Learning Resources - msubbu
e-mail: msubbu.in[AT]gmail.com
Web: http://www.msubbu.in