Euler's Equation of Motion

Home -> Lecture Notes -> Fluid Mechanics -> Unit-II

Mass in per unit time = rAv =

For steady flow, mass out per unit time =

Rate of momentum in =

Rate of momentum out =

Rate of increase of momentum from AB to CD = = rAv dv à 1

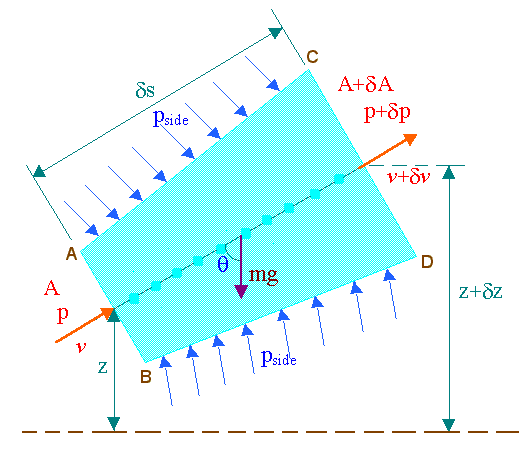
Force due to p in the direction of motion = pA

Force due to p + dp opposing the direction of motion = (p + dp)(A + dA)

Force due to p_side producing a component in the direction of motion = p_sidedA

Force due to mg producing a component opposing the direction of motion = mgcos(q)

Resultant force in the direction of motion = pA - (p + dp)(A + dA) + p_sidedA - mgcos(q) à 2

The value of p_side will vary from p at AB to p + dp at CD, and can be taken as p + kdp where k is fraction.

Mass of fluid element ABCD = m = rg(A + 1/2 dA) ds

And ds = dz/cos(q); since cos(q) = dz/ds

Substituting in equn.2,

Resultant force in the direction of motion = pA - (p + dp)(A + dA) + p + kdp - rg(A + 1/2 dA) dz

= -Adp - dpdA + kdpdA - rgAdz - 1/2 dAdz

Neglecting products of small quantities,

Resultant force in the direction of motion = -Adp - rgAdz à 3

Applying Newton's second law, (i.e., equating equns.1 & 3)

rAv dv = -Adp - rgAdz

dividing by rAds,

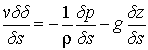
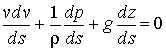
or, in the limit as ds à 0,

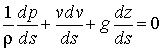
This is known as Euler's equation, giving, in differential form

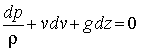
the relationship between p, v, r and elevation z, along a streamline for steady flow.

It can not be integrated until the relationship density and pressure is known.

For incompressible fluid, r is constant; therefore the Euler's equation is integrated to give the following:

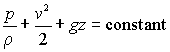
which is nothing but the Bernoulli equation.