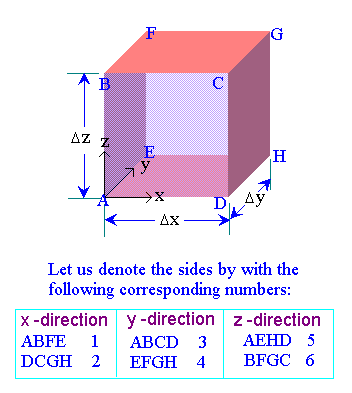
Let us make the mass balance for a fluid element as shown below: (an open-faced cube)

Mass balance:
The mass in the system at any instant is r Dx Dy Dz. The flow into the system through face 1 is
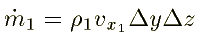
and the flow out of the system through face 2 is
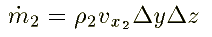
Similarly for the fcaes 3, 4, 5, and 6 are written as follows:
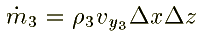
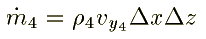
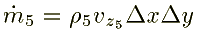
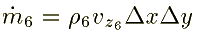
Substituting these quantities in equn.1, we get
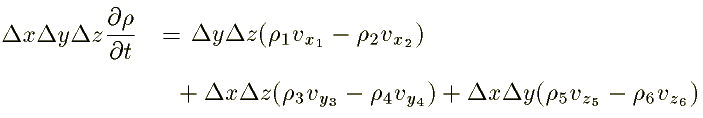
Dividing the above equation by Dx Dy Dz:
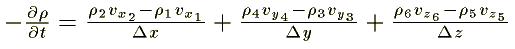
Now we let Dx, Dy, and Dz each approach zero simulaneously, so that the cube shrinks to a point. Taking the limit of the three ratios on the right-hand side of this equation, we get the partial derivatives.
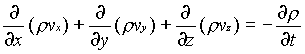
This is the continuity equation for every point in a fluid flow whether steady or unsteady , compressible or incompressible.
For steady, incompressible flow, the density r is constant and the equation simplifies to
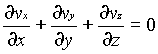
For two dimensional incompressible flow this will simplify still further to
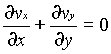
Last Modified on: 14-Sep-2014
Chemical Engineering Learning Resources - msubbu
e-mail: msubbu.in[AT]gmail.com
Web: http://www.msubbu.in