Pascal's law for pressure at a point

Home -> Lecture Notes -> Fluid Mechanics -> Unit-I

The basic property of a static fluid is pressure. Pressure is familiar as a surface force exerted by a fluid against the walls of its container. Pressure also exists at every point within a volume of fluid. For a static fluid, as shown by the following analysis, pressure turns to be independent direction.

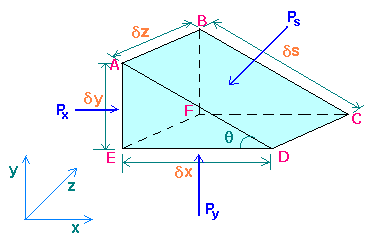
By considering the equilibrium of a small fluid element in the form of a triangular prism ABCDEF surrounding a point in the fluid, a relationship can be established between the pressures P_x in the x direction, P_y in the y direction, and Ps normal to any plane inclined at any angle q to the horizontal at this point.

P_x is acting at right angle to ABEF, and Py at right angle to CDEF, similarly P_s at right angle to ABCD.

Since there can be no shearing forces for a fluid at rest, and there will be no accelerating forces, the sum of the forces in any direction must therefore, be zero. The forces acting are due to the pressures on the surrounding and the gravity force.

Force due to P_x = P_x x Area ABEF = P_xdydz

Horizontal component of force due to P_s = - (P_s x Area ABCD) sin(q) = - P_sdsdz dy/ds = -P_sdydz

As P_y has no component in the x direction, the element will be in equilibrium, if

P_xdydz + (-P_sdydz) = 0

i.e. P_x = P_s

Similarly in the y direction, force due to P_y = P_ydxdz

Component of force due to P_s = - (P_s x Area ABCD) cos(q) = - P_sdsdz dx/ds = - P_sdxdz

Force due to weight of element = - mg = - rVg = - r (dxdydz/2) g

Since dx, dy, and dz are very small quantities, dxdydz is negligible in comparison with other two vertical force terms, and the equation reduces to,

P_y = P_s

Therefore, P_x = P_y = P_s

i.e. pressure at a point is same in all directions. This is Pascal's law. This applies to fluid at rest.

Fine powdery solids resemble fluids in many respects but differs considerably in others. For one thing, a static mass of particulate solids, can support shear stresses of considerable magnitude and the pressure is not the same in all directions.