Fluid Mechanics - Class Test Questions
Home ->
ChE Learning Resources
-> Question Bank
4HE - Fluid Mechanics
Test - 2 (March-2001) Maximum Marks : 60
Duration : 90 minutes
Part A (12 x 2 = 24 Marks)
- With a neat sketch, compare the velocity profiles for laminar and turbulent flow of a fluid in
a pipeline.
- Indicate the methods to reduce
(i) skin frictional losses
(ii) form frictional losses.
- Calculate the hydraulic radius for flow of fluid through a rectangular duct of size 0.5 m x 0.3 m.
- With a neat diagram, illustrate the relation between friction factor and Reynolds number, for laminar and turbulent flows in circular ducts, indicating the effect of roughness.
- The relation between frictional pressure drop (Dp) and volumetric flow rate (Q) for
flow through pipelines is given by
Dp = cQn ; where c is a constant.
What is the value of 'n' for (i) laminar flow
(ii) turbulent flow through very smooth pipe
(iii) turbulent flow through very rough pipe
- Draw the shape of nozzles, that is needed for accelerating the flow velocity, for the following flow conditions, indicating the flow direction:
(i) subsonic flow to soinc flow
(ii) sonic to supersonic flow
(iii) subsonic to supersonic flow
- Draw a neat sketch showing the development of boundary layer for laminar flow in pipe, also indicate the
shape of the velocity profiles at developing and developed sections.
- How does the pressure drop vary with the flow rate in a rota-meter, and in orifice meter?
- The pressure drop between upstream and throat of venturi meter is 100 cm of the flowing fluid. What is the pressure drop
if the volumetric flow rate is doubled?
- Compare the manometer readings of orifice meter and venturi meter
for a flowrate of Q through a pipe of diameter D, given that diameter of venturi throat = diameter of orifice opening.
- Give two industrial applications of:
(i) packed beds
(ii) fluidized beds
- Differentiate between aggregative and particulate fluidization.
Part B (3 x 12 = 36 Marks)
- (a) By applying momentum balance to the steady flow of a fluid in a stream-tube, derive Eulers equation of motion. (8)
(b) Obtain Bernoulli equation from Euler equation by making necessary
assumptions. (4)
Or
- For laminar flow of a Newtonian fluid in circular pipe, obtain the following relations from first principles:
(i) Frictional pressure drop and wall shear stress
(ii) Velocity distribution in the radial direction
(iii) Average velocity and maximum velocity
(iv) Pressure drop and average velocity
- Water is pumped from a ground level reservoir to an overhead tank through a 7.5 cm ID pipe as shown in the sketch:
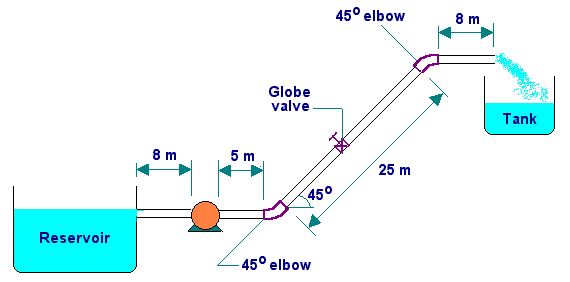
(a) What pressure is needed at the outlet of the pump to supply water to the
tank at the rate of 100 ltr/min?
(b) What is the power required for the pump, if the pump is only 60% efficient?
Data:
m = 1 cP; r = 1 g/ml.
Equivalent length of fittings (Le/D):
Globe valve (open) : 300
45o elbow : 15
Fanning friction factor for turbulent flow is given by: f = 0.079 (NRe)-0.25
Or
-
(a) A venturi meter has throat to upstream pipe cross-section ratio of 0.5.
The fluid flowing is water. The pressure at the entry of converging cone
section is 137.9 kN/m2(a).
What is the velocity at the throat which corresponds to a
pressure of 0 kN/m2(a) at the throat?
If the water is at 200oF,
what is the highest velocity possible at the throat at which water
will boil?
Data: For water at 200oF,
Density = 980 kg/m3.
Vapor pressure = 75.8 kN/m2(a). (8)
(b) A rotameter with a stainless steel float has a maximum capacity of 1.2 ltr/sec of water.
What will be the maximum capacity for kerosene in ltr/sec for the same rotameter and float? Assume that the Cd for the rotameter is not
changing much with flowrate.
Data:
Specific gravity of stainless steel = 7.92
Specifc gravity of kerosene = 0.82 (4)
- (a) Derive relations for Reynolds number and friction factor and
establish the Ergun equation for single-phase flow of fluid through
packed bed. (8)
(b) Bring out the equation predicting minimum fluidization velocity.
(4)
Or
- A mixture of vapors pass through a packed bed of glass spheres having density 2.4 g/cc each
of diameter 0.5 cm. The pressure drop due to the flow is 4000 N/m2. The height of packed bed
is 1.85 m. The density and viscosity of the vapor mixture are 3.8 x 10-3 g/cc and 0.015 cP
respectively.
Data:
Cross sectional area of the packed column tube = 0.09
m2
Bed porosity = 0.4
Find the mass flow rate of the vapor mixture.
[Index] [ Get More Questions with Solutions from Our Online Course...]
Last Modified on: 04-Feb-2022
Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in
