0200-11-td-1mark

Entropy change for an irreversible process, taking into account both the system and surroundings together, is:

• Positive
• Negative
• Zero
• None of these

0200-12-td-1mark

Mixing of two fluids is a

• Reversible process
• Irreversible process
• Isothermal process
• None of these

GATE-CH-1991-7-v-td-2mark

The shape of \(T\)-\(S\) diagram for Carnot cycle is

• a rectangle

• a rhombus

• a trapezoid

• a circle

GATE-CH-1993-5-d-td-1mark

A reversible heat transfer demands:

• The temperature difference causing heat transfer tends to zero

• The system receiving heat must be at a constant temperature

• The system transferring out heat must be at a constant temperature

• Both interacting systems must be at constant temperatures

GATE-CH-1993-5-f-td-1mark

When a system executes an irreversible cycle:

• \(\oint dQ/T < 0\)

• \(\oint dS > 0\)

• \(\oint dS = 0\)

• \(\oint dQ/T > 0\)

GATE-CH-1994-1-t-td-1mark

The second law of thermodynamics states that

• the energy change of a system undergoing any reversible process is zero

• it is not possible to transfer heat from a lower temperature to a higher temperature

• the total energy of the system and surroundings remains constant

• none of the above

GATE-CH-1995-1-n-td-1mark

The kinetic energy of gas molecules is zero at

• 0\(^\circ \)C

• 273\(^\circ \)C

• 100\(^\circ \)C

• \(-273^\circ \)C

GATE-CH-1995-2-r-td-2mark

A closed system is cooled reversibly from 100\(^\circ \)C to 50\(^\circ \)C. If no work is done on the system

• its internal energy (\(U\)) decreases and its entropy (\(S\)) increases

• \(U\) and \(S\) both decrease

• \(U\) decreases but \(S\) is constant

• \(U\) is constant but \(S\) decreases

GATE-CH-1997-1-19-td-1mark

A system undergoes a change from a given initial state to a given final state either by an irreversible process or by a reversible process. Then ---------------
where \(\Delta S_I\) and \(\Delta S_R\) are the entropy changes of the system for the irreversible and reversible processes, respectively.

• \(\Delta S_I\) is always \( > \Delta S_R\)

• \(\Delta S_I\) is sometimes \( > \Delta S_R\)

• \(\Delta S_I\) is always \( < \Delta S_R\)

• \(\Delta S_I\) is always \( = \Delta S_R\)

GATE-CH-2000-1-6-td-1mark

On a \(P\)-\(V\) diagram of an ideal gas, suppose a reversible adiabatic line intersects a reversible isothermal line at point \(A\). Then at point \(A\), the slope of the reversible adiabatic line \((\partial P/\partial V)_S\) and the slope of the reversible isothermal line  \((\partial P/\partial V)_T\)  are related as _________ (where \(\gamma = C_P/C_V\))

• \((\partial P/\partial V)_S = (\partial P/\partial V)_T\)

• \((\partial P/\partial V)_S = [(\partial P/\partial V)_T]^\gamma\)

• \((\partial P/\partial V)_S = \gamma (\partial P/\partial V)_T\)

• \((\partial P/\partial V)_S = (1/\gamma)(\partial P/\partial V)_T\)

GATE-CH-2003-45-td-2mark

The following heat engine produces power of 100,000 kW. The heat engine operates between 800 K and 300 K. It has a thermal efficiency equal to 50% of that of the Carnot engine for the same temperatures. The rate at which heat is absorbed from the hot reservoir is

• 100,000 kW

• 160,000 kW

• 200,000 kW

• 320,000 kW

GATE-CH-2004-46-td-2mark

A cyclic engine exchanges heat with two reservoirs maintained at 100 and 300^oC , respectively. The maximum work (in J) that can be obtained from 1000 J of heat extracted from the hot reservoir is

• 349

• 651

• 667

• 1000

GATE-CH-2005-7-td-1mark

Which one of the following statements is TRUE?

• Heat can be fully converted into work

• Work cannot be fully converted into heat

• The efficiency of a heat engine increases as the temperature of the heat source is increased while keeping the temperature of the heat sink fixed

• A cyclic process can be devised whose sole effect is to transfer heat from a lower temperature to a higher temperature

GATE-CH-2006-6-td-1mark

A heat engine operates at 75% of the maximum possible efficiency. The ratio of the heat source temperature (in K) to the heat sink temperature (in K) is 5/3. The fraction of the heat supplied that is converted to work is

• 0.2

• 0.3

• 0.4

• 0.6

GATE-CH-2006-7-td-1mark

For the isentropic expansion of an ideal gas from the initial conditions \(P_1,T_1\) to the final conditions \(P_2,T_2\), which ONE of the following relations is valid (\(\gamma = C_P/C_V\))

• \(\displaystyle \frac {P_1}{P_2} = \left (\frac {T_2}{T_1}\right )^\gamma \)

• \(\displaystyle \frac {P_1}{P_2} = \left (\frac {T_1}{T_2}\right )^{\frac {\gamma }{\gamma -1}}\)

• \(\displaystyle \frac {P_1}{P_2} =\frac {T_2}{T_1}\)

• \(\displaystyle \frac {P_1}{P_2} = \left (\frac {T_1}{T_2}\right )^{\frac {\gamma -1}{\gamma }}\)

GATE-CH-2007-32-td-2mark

Which one of the following represents the Carnot cycle (ideal engine) ?

• 
• 
• 
• 

GATE-CH-2007-7-td-1mark

The change in entropy of the system, \(\Delta S_{\text {sys}}\), undergoing a cyclic irreversible process is

• greater than zero

• equal to zero

• less than zero

• equal to the \(\Delta S_{\text {surroundings}}\)

GATE-CH-2012-8-td-1mark

In a parallel flow heat exchanger operating under steady state, hot liquid enters at a temperature \(T_{\text {h,in}}\) and leaves at \(T_{\text {h,out}}\). Cold liquid enters at a temperature of \(T_{\text {c,in}}\) and leaves at a temperature \(T_{\text {c,out}}\). Neglect any heat loss from the heat exchanger to the surrounding. If \(T_{\text {h,in}} \gg T_{\text {c,in}}\), then for a given time interval, which ONE of the following statements is true?

• Entropy gained by the cold stream is GREATER than entropy lost by the hot stream

• Entropy gained by the cold stream is EQUAL to the entropy lost by the hot stream

• Entropy gained by the cold stream is LESS than the entropy lost by the hot stream

• Entropy gained by the cold stream is ZERO

GATE-CH-2013-30-td-2mark

In a process occurring in a closed system \(F\), the heat transferred from \(F\) to the surroundings \(E\) is 600 J. If the temperature of \(E\) is 300 K and that of \(F\) is in the range 380-400 K, the entropy changes of the surroundings \((\Delta S_E)\) and system \((\Delta S_F)\), in J/K, are given by

• \(\Delta S_E = 2, \Delta S_F = -2\)

• \(\Delta S_E = -2,\Delta S_F = 2\)

• \(\Delta S_E= 2, \Delta S_F < -2\)

• \(\Delta S_E= 2, \Delta S_F > -2\)

GATE-CH-2017-7-td-1mark

Water is heated at atmospheric pressure from 40^oC to 80^oC using two different processes. In process I, the heating is done by a source at 80^oC. In process II, the water is heated from 40^oC to 60^oC by a source at 60^oC, and then from 60^oC to 80^oC by another source at 80^oC .

Identify the correct statement.

• Enthalpy change of water in process I is greater than enthalpy change in process II

• Enthalpy change of water in process II is greater than enthalpy change in process I

• Process I is closer to reversibility

• Process II is closer to reversibility

GATE-ME-2009-30-td-2mark

An irreversible heat engine extracts heat from a high temperature source at a rate of 100 kW and rejects heat to a sink at a rate of 50 kW. The entire work output of the heat engine is used to drive a reversible heat pump operating between a set of independent isothermal heat reservoirs at 17^oC and 75^oC. The rate (in kW) at which the heat pump delivers heat to its high temperature sink is

• 50

• 250

• 300

• 360

GATE-ME-2012-A-19-td-1mark

An ideal gas of mass \(m\) and temperature \(T_1\) undergoes a reversible isothermal process from an initial pressure \(P_1\) to final pressure \(P_2\). The heat loss during the process is \(Q\). The entropy change \(\Delta S\) of the gas is

• \(\displaystyle mR\ln \left (\frac {P_2}{P_1}\right )\)

• \(\displaystyle mR\ln \left (\frac {P_1}{P_2}\right )\)

• \(\displaystyle mR\ln \left (\frac {P_2}{P_1}\right )-\frac {Q}{T_1}\)

• zero

GATE-XE-2009-E-9-td-2mark

Atmospheric air (\(R=287\) J/kg.K; \(\gamma =1.4\)) at 1 bar and 25^oC is compressed adiabatically to 2 bar and 105^oC . Which of the following statements is correct?

• The process is possible but irreversible

• The process is possible and reversible

• The process is impossible

• The process is possible and isentropic

GATE-XE-2010-E-4-td-1mark

A heat pump, which operates in a cycle, extracts heat energy from the cold reservoir and supplies the same amount of energy to the hot reservoir. Which of the following statements holds for this process?

• This process violates both the first and the second law

• This process violates the first law but not the second law

• This process violates the second law but not the first law

• This process does not violate both first and second law

GATE-XE-2013-E-4-td-1mark

For a reversible isothermal expansion of an ideal gas from a state 1 to a state 2,

• \(S_1=S_2\)

• \(S_1>S_2\)

• \(S_1<S_2\)

• \(H_1>H_2\)

GATE-CH-1994-3-r-td-1mark

A process is irreversible as long as entropy change (\(\Delta S\)) for the system is greater than zero. (True/False)

• True
• False

GATE-CH-1992-17-a-td-3mark

\(10^6\) Joules of heat are transferred from a reservoir at 327\(^\circ \)C to an engine that operates on the Carnot cycle. The engine rejects heat to a reservoir at 27\(^\circ \)C. Determine: (i) the thermal efficiency of the cycle (%), and (ii) the work done (in MJ) by the engine.
(i) {#1}

(ii) {#2}

GATE-CH-2003-44-td-2mark

A solid metallic block weighing 5 kg has an initial temperature of 500^oC; 40 kg of water initially at 25^oC is contained in a perfectly insulated tank. The metallic block is brought into contact with water. Both of them come to equilibrium. Specific heat of block material is 0.4 kJ kg^-1.K^-1. Ignoring the effect of expansion and contraction, and also the heat capacity of tank, the total entropy change in kJ.K^-1 is

• -1.87

• 0.0

• 1.26

• 3.91

GATE-CH-2005-44-td-2mark

A Carnot heat engine cycle is working with an ideal gas. The work performed by the gas during the adiabatic expansion and compression steps, \(W_1\) and \(W_2\) respectively, are related as

• \(|W_1| > |W_2|\)

• \(|W_1| < |W_2|\)

• \(W_1=W_2\)

• \(W_1=-W_2\)

GATE-ME-2007-37-td-2mark

A heat transformer is a device that transfers a part of the heat, supplied to it at an intermediate temperature, to a high temperature reservoir while rejecting the remaining part to a low temperature heat sink. In such a heat transformer, 100 kJ of heat is supplied at 350 K. The maximum amount of heat in kJ that be transferred to 400 K, when the rest is rejected to a heat sink at 300 K is

• 12.50

• 14.29

• 33.33

• 57.14

GATE-ME-2008-47-td-2mark

A cyclic device operates between three thermal reservoirs, as shown in the figure. Heat is transferred to/from the cyclic device. It is assumed that heat transfer between each thermal reservoir and the cyclic device takes place across negligible temperature difference. Interactions between the cyclic device and the respective thermal reservoirs that are shown in the figure are all in the form of heat transfer.

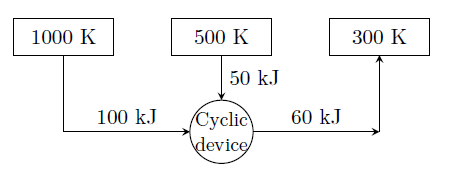
The cyclic device can be

• a reversible heat engine

• a reversible heat pump or a reversible refrigerator

• an irreversible heat engine

• an irreversible heat pump or an irreversible refrigerator

GATE-ME-2010-40-td-2mark

Consider the following two processes:

• [(I)] A heat source at 1200 K loses 2500 kJ of heat to a sink at 800 K
• [(II)] A heat source at 800 K loses 2000 kJ of heat to a sink at 500 K

Which of the following statements is true?

• Process I is more irreversible than Process II

• Process II is more irreversible than Process I

• Irreversibility associated in both the processes are equal

• Both the processes are reversible

GATE-CH-1993-6-3-td-2mark

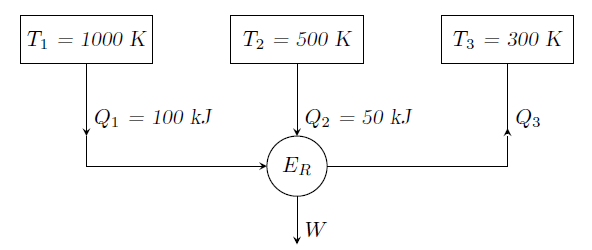
Figure below shows a reversible heat engine \(E_R\) having heat interactions with three constant temperature systems. Calculate the thermal efficiency (in %) of the heat engine.

• Answer

GATE-CH-1995-24-td-5mark

Calculate the change in entropy (cal/g.\(^\circ \)C) when one gram of ice at 0\(^\circ \)C is converted into steam at 100\(^\circ \)C.
The latent heat of fusion of ice = 80 cal/g. Latent heat of vaporization of water = 540 cal/g and the mean specific heat of water between 0\(^\circ \)C and 100\(^\circ \)C = 1 cal/(g.\(^\circ \)C).

• Answer

GATE-XE-2010-E-21-22-td-4mark

In a process industry, two different streams of water (to be considered incompressible) are available at 10^oC and 90^oC as shown in the figure. Mass flow rates of both the streams are 1 kg/s. Rather than wasting these resources, it is desired to connect a reversible Carnot engine that will continuously extract heat from the hot stream and supply part of it to the cold stream such that the exit temperatures of both the streams \(T_f\) is identical. Heat capacity of water is 4.18 kJ/(kg.K).

(i) Value of \(T_f\) is

{#1}

(ii) Work output \(\dot {W}\) is

{#2}

GATE-CH-1992-17-b-td-3mark

An inventor claims to have developed a refrigeration unit which maintains the refrigerated space at \(-3\)\(^\circ \)C while operating in a room where the temperature is 27\(^\circ \)C, and which has a coefficient of performance of 9.5. How do you evaluate his claim?

• Answer

GATE-ME-2008-71-72-73-td-6mark

In the figure shown, the system is a pure substance kept in a piston-cylinder arrangement. The system is initially a two-phase mixture containing 1 kg of liquid and 0.03 kg of vapor at a pressure of 100 kPa. Initially, the piston rests on a set of stops, as shown in the figure. A pressure of 200 kPa is required to exactly balance the weight of the piston and the outside atmospheric pressure. Heat transfer takes place into the system until its volume increases by 50%. Heat transfer to the system occurs in such a manner that the piston, when allowed to move, does so in a very slow (quasi-static/quasi-equilibrium) process. The thermal reservoir from which heat is transferred to the system has a temperature of 400^oC. Average temperature of the system boundary can be taken as 175^oC. The heat transfer to the system is 1 kJ, during which its entropy increases by 10 J/K.

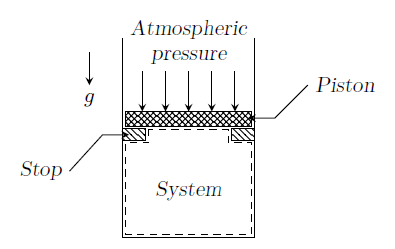
Specific volumes of liquid (\(V_L\)) and vapor (\(V_V\)) phases, as well as values of saturation temperatures, are given in the table below.

Pressure (kPa)	Saturation temperature \(T_{\text{sat}}\) ( \(^\circ\)C)	\(V_L\) (m\(^3\)/kg)	\(V_V\) (m\(^3\)/kg)
100	100	0.001	0.1
200	200	0.0015	0.002

(i) At the end of the process, which one of the following situations will be true?

{#1}

(ii) The work done by the system during the process is

{#2}

(iii) The net entropy generation (considering the system and the thermal reservoir together) during the process is closest to

{#3}