Mass Transfer - GATE-CH Questions
Home -> GATE Questions with Solutions at MSubbu.Academy -> Mass Transfer->
Convective Mass Transfer
0600-2-mt-1mark
Sherwood number in mass transfer is analogous to the following dimensionless group in heat transfer
GATE-CH-1990-5-i-mt-2mark
In the absorption of a solute gas from a mixture containing inerts in a solvent, it has been found that the overall gas transfer coefficient is nearly equal to the individual gas film transfer coefficient. It may therefore be concluded that:
GATE-CH-1994-1-p-mt-1mark
Mass transfer coefficient, \(k\), according to penetration theory varies with mass diffusivity as
GATE-CH-1995-2-p-mt-2mark
For absorbing sparingly soluble gas in a liquid
GATE-CH-1997-1-16-mt-1mark
For turbulent mass transfer in pipes, the Sherwood number depends upon the Reynolds number(\(\text {Re}\)) as
[Index]
GATE-CH-1997-2-13-mt-2mark
According to the film theory of mass transfer, the mass transfer coefficient is proportional to (where \(D\) is the molecular diffusivity)
GATE-CH-1998-1-16-mt-1mark
The mass transfer coefficient for a solid sphere of radius ‘\(a\)’, dissolving in a large volume of quiescent liquid, in which \(D\) is the diffusivity of the solute, is
GATE-CH-1998-1-17-mt-1mark
In an interphase mass transfer process, the lesser the solubility of a given solute in a liquid, the higher are the chances that the transfer process will be
GATE-CH-1998-2-14-mt-2mark
If the Prandtl number is greater than the Schmidt number,
GATE-CH-1998-2-19-mt-2mark
In an interphase heat transfer process, the equilibrium state corresponds to equality of temperatures in the two phases, while the condition for equilibrium in an interpahse mass transfer process is
[Index]
GATE-CH-1999-1-19-mt-1mark
Penetration theory states that the mass transfer coefficient is equal to (where \(D_e\) is diffusivity and \(t\) is time)
GATE-CH-2001-1-11-mt-1mark
The surface renewal frequency in Danckwerts’ model of mass transfer is given by (\(k_L\): mass transfer coefficient, m/s)
GATE-CH-2001-1-12-mt-1mark
For gas absorption the height of a transfer unit, based on the gas phase, is given by (\(G\): superficial molar gas velocity; \(L\): superficial molar liquid velocity; \(F_G\): mass transfer coefficient, mol/m2.s; \(a\): interfacial area per unit volume of tower)
GATE-CH-2002-1-24-mt-1mark
The dimensionless group in mass transfer that is equivalent to Prandtl number in heat transfer is
GATE-CH-2002-1-25-mt-1mark
The Reynolds analogy for momentum, heat and mass transfer is best applicable for
[Index]
GATE-CH-2003-64-mt-2mark
The Reynolds number of the liquid was increased 100 fold for a laminar film used for gas-liquid contacting. Assuming penetration theory is applicable, the fold-increase in the mass transfer coefficient (\(k_c\)) for the same system is
GATE-CH-2005-21-mt-1mark
For turbulent flow past a flat plate, when no form drag is present, the friction factor \(f\) and the Chilton-Colburn factor \(j_D\) are related as
GATE-CH-2005-65-mt-2mark
Match the variation of mass transfer coefficient given by the theory in Group I with the appropriate variation in Group II.
| Group I |
Group II |
| (P) Film Theory |
(1) \(\propto D_{AB}\) |
| (Q) Penetration theory |
(2) \(\propto D_{AB}^{2/3}\) |
| (R) Boundary layer theory |
(3) \(\propto D_{AB}^{1/2}\) |
GATE-CH-2006-43-mt-2mark
Experiments conducted with a sparingly dissolving cylinder wall in a flowing liquid yielded the following correlation for the Sherwood number \[ \text {Sh} = 0.023 (\text {Re})^{0.83} \ (\text {Sc})^{1/3} \] Assuming the applicability of the Chilton-Colburn analogy, the corresponding correlation for heat transfer is
GATE-CH-2010-3-mt-1mark
The ratio of the thermal boundary layer thickness to the concentration boundary layer thickness is proportional to
[Index]
GATE-CH-2011-20-mt-1mark
Simultaneous heat and mass transfer is occurring in a fluid flowing over a flat plate. The flow is laminar. The concentration boundary layer will COINCIDE with the thermal boundary layer, when
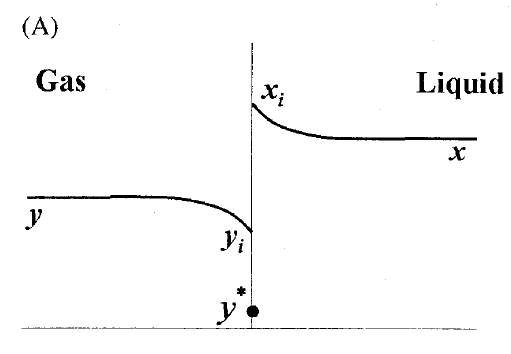
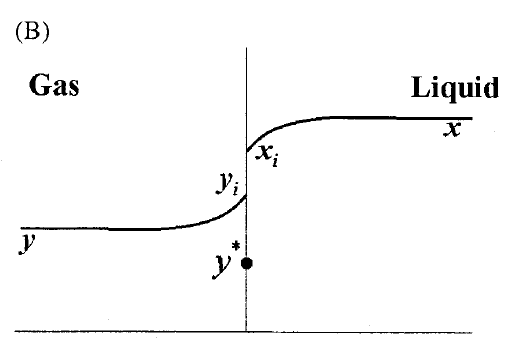
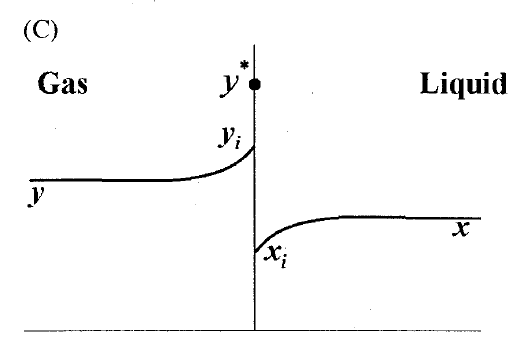
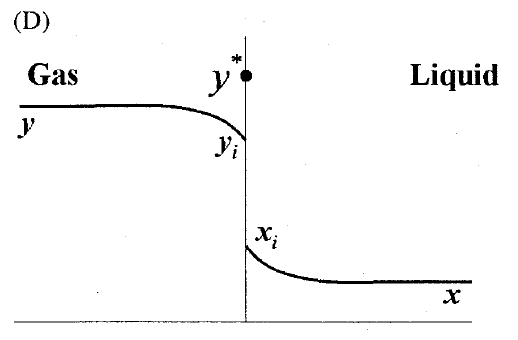
GATE-CH-2011-40-mt-2mark
A gas mixture is in contact with a liquid. Component \(P\) in the gas mixture is highly soluble in the liquid. Possible concentration profiles during absorption of \(P\) are shown in choices, where
\(x\) : mole fraction of \(P\) in bulk liquid
\(y\) : mole fraction of \(P\) in bulk gas
\(x_i\) : mole fraction of \(P\) at the interface in liquid
\(y_i\) : mole fraction of \(P\) at the interface in gas
\(y^*\) : equilibrium gas phase mole fraction corresponding to \(x_i\)
The CORRECT profile is
GATE-CH-2012-18-mt-1mark
For which of the following operations, does the absorption operation become gas-film controlled?
- [P.] The solubility of gas in the liquid is very high
- [Q.] The solubility of gas in the liquid is very low
- [R.] The liquid-side mass transfer coefficient is much higher than the gas-side mass transfer coefficient
- [S.] The liquid-side mass transfer coefficient is much lower than the gas-side mass transfer coefficient
GATE-CH-2014-19-mt-1mark
Assuming the mass transfer coefficients in the gas and the liquid phases are comparable, the absorption of CO2 from reformer gas (CO2+H2) into an aqueous solution of diethanolamine is controlled by
GATE-CH-2014-20-mt-1mark
Which ONE of the following statements is CORRECT for the surface renewal theory?
[Index]
GATE-CH-2016-12-mt-1mark
Match the dimensionless numbers in Group-1 with the ratios in Group-2.
| Group-1 |
Group-2 |
| P. Biot number |
I. \(\dfrac {\text {buoyancy force}}{\text {viscous force}}\) |
| Q. Schmidt number |
II. \(\dfrac {\text {internal thermal resistance of a solid}}{\text {boundary layer thermal resistance}}\) |
| R. Grashof number |
III. \(\dfrac {\text {momentum diffusivity}} {\text {mass diffusivity}}\) |
GATE-CH-2017-16-mt-1mark
Consider steady state mass transfer of a solute \(A\) from a gas phase to a liquid phase. The gas phase bulk and interface mole fractions are \(y_{A,G}\) and \(y_{A,i}\), respectively. The liquid phase bulk and interface mole fractions are \(x_{A,L}\) and \(x_{A,i}\), respectively. The ratio \(\dfrac {(x_{A,i}-x_{A,L})}{(y_{A,G}-y_{A,i})}\) is very close to zero. This implies that mass transfer resistance is
GATE-CH-2017-43-mt-2mark
The Sherwood number (Sh\(_{L}\)) correlation for laminar flow over a flat plate of length \(L\) is given by \[ \text {Sh}_{L} = 0.664\; \text {Re}_L^{0.5}\; \text {Sc}^{1/3} \] where Re\(_L\) and Sc represent Reynolds number and Schmidt number, respectively. This correlation, expressed in the form of Chilton-Colburn \(j_D\) factor, is
GATE-CH-1994-3-k-mt-1mark
Forced convection is relatively more effective in increasing the rate of mass transfer if Schmidt number is larger. (True/False)
GATE-CH-1994-20-mt-5mark
A stream of air at 100 kPa pressure and 300 K is flowing on the top surface of a thin flat sheet of solid naphthalene of length 0.2 m with a velocity of 20 m/s.
The other data are:
Mass diffusivity of naphthalene vapor in air = \(6 \times 10^{-6}\) m\(^2\)/s
Kinematic viscosity of air = \(1.5 \times 10^{-5}\) m\(^2\)/s
Concentration of naphthalene at the air-solid naphthalene interface = \(1 \times 10^{-5}\) kmol/m\(^3\)
Note: For heat transfer over a flat plate, convective heat transfer coefficient for laminar flow can be calculated by the equation: \[ \text {Nu} = 0.664 \text {Re}_L^{1/2} \text {Pr}^{1/3} \] You may use analogy between mass and heat transfer.
Calculate:
(a) the average mass transfer coefficient( in m/s) over the flat plate
{#1}
(b) the rate of loss of naphthalene from the surface per unit width (in mol.m\(^{-1}\).h\(^{-1}\))
{#2}
[Index]
GATE-CH-2004-19-20-mt-2mark
Pure aniline is evaporating through a stagnant air film of 1 mm thickness at 300 K and a total pressure of 100 kPa. The vapor pressure of aniline at 300 K is 0.1 kPa. The total molar concentration under these conditions is 40.1 mol/m3. The diffusivity of aniline in air is \(0.74 \times 10^{-5}\) m2/s.
(i) The numerical value of the mass transfer coefficient is \(7.4\times 10^{-3}\). Its units are
{#1}
(ii) The rate of evaporation of aniline is \(2.97 \times 10^{-4}\). Its units are
{#2}
GATE-CH-2000-2-14-mt-2mark
The individual mass transfer coefficients (mol/m2.s) for absorption of a solute from a gas mixture into a liquid solvent are \(k_x\) =4.5 and \(k_y\) = 1.5. The slope of the equilibrium line is 3. Which of the following resistance(s) is (are) controlling?
GATE-CH-2001-2-12-mt-2mark
The interfacial area per unit volume of dispersion, in a gas-liquid contactor, for fractional hold-up of gas = 0.1 and gas bubble diameter = 0.5 mm is given by (in m2/m3)
GATE-CH-2005-64-mt-2mark
Two solid discs of benzoic acid (molecular weight = 122) of equal dimensions are spinning separately in large volumes of water and air at 300 K. The mass transfer coefficients for benzoic acid in water and air are \(0.9 \times 10^{-5}\) and \(0.47 \times 10^{-2}\) m/s respectively. The solubility of benzoic acid in water is 3 kg/m3 and the equilibrium vapor pressure of benzoic acid in air is 0.04 kPa. Then the disc
GATE-CH-2008-52-mt-2mark
A sparingly soluble solute in the form of a circular disk is dissolved in an organic solvent as shown in the figure. The area available for mass transfer from the disk is \(A\) and the volume of the initially pure organic solvent is \(V\). The disk is rotated along the horizontal plane at a fixed rpm to produce a uniform concentration of the dissolving solute in the liquid. The convective mass transfer coefficient under these conditions is \(k_c\). The equilibrium concentration of the solute in the solvent is \(C^*\). The time required for the concentration to reach 1% of the saturation value is given by
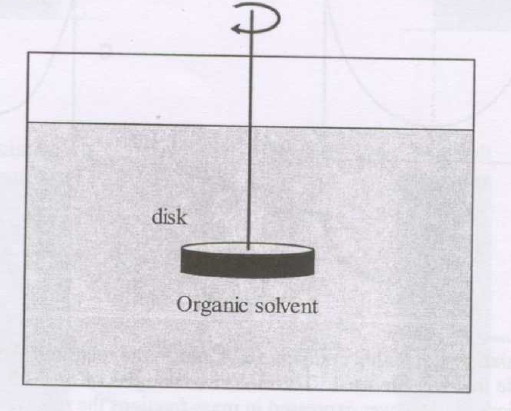
[Index]
GATE-CH-2014-31-mt-2mark
A spherical ball of benzoic acid (diameter = 1.5 cm) is submerged in a pool of still water. The solubility and diffusivity of benzoic acid in water are 0.03 kmol/m3 and \(1.25 \times 10^{-9}\) m2/s respectively. Sherwood number is given as \(\text {Sh} = 2.0 + 0.6 \text {Re}^{0.5}\text {Sc}^{0.33}\). The initial rate of dissolution (in kmol/s) of benzoic acid approximately is
GATE-CH-1991-6-i-mt-2mark
The diffusion rate of ammonia from an aq.solution to the gas phase is \(10^{-3}\) kmol/m\(^2\).s. The interface equilibrium pressure of \(\ce {NH3}\) is 660 N/m\(^2\) and the concentration of \(\ce {NH3}\) in the gas phase is 5%. If the total pressure is 101 N/m\(^2\), temperature is 295 K and diffusivity of \(\ce {NH3}\) is 0.24 cm\(^2\)/s, the gas film thickness is ____________(\(\mu \)m).
GATE-CH-2001-13-mt-5mark
A sugary substance \(A\) is added to a pot of milk (initially containing no \(A\)) and stirred vigorously by a spoon so that the concentration of \(A\), \(C_A\), is uniform everywhere. The mass transfer coefficient for the transfer of \(A\) into the liquid is \(k_{sl} = 1\times10^{-4}\) m/s. Solid \(A\) is added in great excess compared to the saturation capacity of milk to dissolve \(A\). Assume that the solid-liquid interfacial area stays constant throughout the dissolution process and is given by \(a=1000\) cm\(^2\). Derive the expression for \(C_A\) versus time, \(t\). The time (in s) taken for \(C_A/C_A^*=0.95\) ___________
\(C_A^* = 5\times10^{-2}\) kmol/m\(^3\); \(V_L\) = 1000 cm\(^3\).
GATE-CH-2002-12-mt-5mark
The mass flux from a 5 cm diameter naphthalene ball, placed in stagnant air at 40\(^\circ\)C and atmospheric pressure, is \(1.47 \times 10^{-3}\) mol/m\(^2\).s. Assume the vapor pressure of naphthalene to be 0.15 atm at 40\(^\circ\)C and negligible bulk concentration of naphthalene in air. If air starts blowing across the surface of naphthalene ball at 3 m/s, by what factor will the mass transfer rate increase, all other conditions remaining the same? _______________
For spheres: \[\text{Sh} = 2.0 + 0.6 (\text{Re})^{0.5} (\text{Sc})^{0.33}\] where \(\text{Sh}\) is the Sherwood number and \(\text{Sc}\) is the Schmidt number. The viscosity and density of air are \(1.8\times10^{-5}\) kg/m.s and 1.123 kg/m\(^3\), respectively and the gas constant is 82.06 cm\(^3\).atm/mol.K
GATE-CH-2013-39-mt-2mark
A study was conducted in which water was pumped through cylindrical pipes made of a sparingly soluble solid. For a given pipe and certain flow conditions, the mass transfer coefficient \(k_c\) has been calculated as 1 mm/s using the correlation \(\text {Sh} = 0.025 \text {Re}^{0.6} \text {Sc}^{0.33}\). If the velocity of the fluid and the diameter of the pipe are both doubled, what is the new value of \(k_c\) in mm/s, up to 2 digits after the decimal point? ____________
[Index]
GATE-CH-1990-15-iii-mt-6mark
Consider a system in which component \(A\) is being transferred from a gas phase to a liquid phase. The equilibrium relation is given by \(y_A = 0.75 x_A\) where \(y_A\) and \(x_A\) are mole fractions of \(A\) in gas and liquid phase respectively. At one point in the equipment, the gas contains 10 mole % \(A\) and liquid 2 mole % \(A\). Gas film mass transfer coefficient \(k_y\) at this point is 10 kmol/(h.m\(^2\).\(\Delta y_A\)) and 60% of the resistance is in the gas film. Calculate:
(a) the overall mass transfer coefficient in kmol/(h.m\(^2\).\(\Delta y_A\)).
{#1}
(b) mass flux of \(A\) in kmol/(h.m\(^2\)).
{#2}
(c) the interfacial gas concentration of \(A\) in mole fraction.
{#3}
GATE-CH-1988-5-a-ii-mt-1mark
A pure gas is absorbed in a solvent in which the gas is highly soluble. The controlling resistance is in the ––––- film.
GATE-CH-1989-5-i-b-mt-1mark
Schmidt number is the ratio of ––––- diffusivity to ––––- diffusivity.
GATE-CH-1989-5-i-c-mt-1mark
Reynolds analogy between momentum and mass transfer is applicable when ––––- number is equal to ––––- .
GATE-CH-1992-6-c-mt-2mark
––––- number in mass transfer corresponds to Nusselt number in heat transfer and ––––- number to Prandtl number.
GATE-CH-1993-12-c-mt-2mark
Associate the following dimensionless groups, with heat transfer, mass transfer and momentum transfer.
- Sherwood number
- Prandtl number
- Nusselt number
- Schmidt number
GATE-CH-1994-2-o-mt-1mark
The Reynolds analogy for mass transfer is given by ––––- and is applicable when Schmidt number is ––––-
[Index]
Last Modified on: 03-May-2024
Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in