GATE-CH-1992-4-a-mo-2mark

A particle \(A\) of diameter 10 microns settles in an oil of specific gravity 0.9 and viscosity 10 poise under Stokes law. A particle \(B\) with diameter 20 microns settling in the same oil will have a settling velocity

• same as that of \(A\)

• one-fourth as that of \(A\)

• twice as that of \(A\)

• four-times as that of \(A\)

GATE-CH-1993-10-b-mo-2mark

For separating particles of different densities, the differential settling method uses a liquid sorting medium of density

• intermediate between those of the light and heavy ones

• less than that of either one

• greater than that of either one

• of any arbitrary value

GATE-CH-1995-1-d-mo-1mark

Jigging is a technique by which different particles can be separated by

• particle size

• particle density

• particle shape

• mixed

GATE-CH-1996-1-7-mo-1mark

Stokes equation is valid in the Reynolds number range

• 0.01 to 0.1

• 0.1 to 2

• 2 to 10

• 10 to 100

GATE-CH-1999-2-6-mo-2mark

Velocity of a small particle of diameter \(D_p\) at a distance \(r\) from the rotational axis of a cyclone rotating at an angular speed \(\omega \) is given by (the other symbols are as per standard notation)

• \(\displaystyle \left (\frac {D_p}{18}\frac {\rho _s-\rho }{\mu }\right )\omega ^2r\)

• \(\displaystyle \left (\frac {D_p^2}{18}\frac {\rho _s-\rho }{\mu }\right )\omega r^2\)

• \(\displaystyle \left (\frac {D_p}{18}\frac {\rho _s-\rho }{\mu }\right )\omega ^2r^2\)

• \(\displaystyle \left (\frac {D_p^2}{18}\frac {\rho _s-\rho }{\mu }\right )\omega ^2r\)

GATE-CH-2000-1-8-mo-1mark

For a sphere falling in a constant drag coefficient regime, its terminal velocity depends on its diameter \(d\) as

• \(d\)

• \(d^{0.5}\)

• \(d^{2}\)

• \(1/d\)

GATE-CH-2004-15-mo-1mark

For a particle settling in water at its terminal settling velocity, which of the following is true?

• buoyancy = weight + drag

• weight = buoyancy + drag

• drag = buoyancy + weight

• drag = weight

GATE-CH-2013-33-mo-2mark

In the elutriation leg of a commercial crystallizer containing a mixture of coarse and very fine crystals of the same material, a liquid is pumped vertically upward. The liquid velocity is adjusted such that it is slightly lower than the terminal velocity of the coarse crystals only. Hence

• the very fine and coarse crystals will both be carried upward by the liquid

• the very fine and coarse crystals will both settle at the bottom of the tube

• the very fine crystals will be carried upward and the coarse crystals will settle

• the coarse crystals will be carried upward and the very fine crystals will settle

GATE-CH-2016-7-mo-1mark

In a cyclone separator used for separation of solid particles from a dust laden gas, the separation factor is defined as the ratio of the centrifugal force to the gravitational force acting on the particle. \(S_r\) denotes the separation factor at a location (near the wall) that is at a radial distance \(r\) from the centre of the cyclone. Which one of the following statements is INCORRECT?

• \(S_r\) depends on mass of the particle

• \(S_r\) depends on the acceleration due to gravity

• \(S_r\) depends on tangential velocity of the particle

• \(S_r\) depends on the radial location (\(r\)) of the particle

GATE-CH-1990-3-iii-mo-2mark

Two very small silica particles are settling at their respective terminal velocities through a highly viscous oil column. If one particle is twice as large as the other, the larger particle will take ––––- times the time than by the smaller particle to fall through the same height.

• Answer

GATE-CH-2013-15-mo-1mark

Separation factor of a cyclone 0.5 m in diameter and having a tangential velocity of 20 m/s near the wall is ____________(Take \(g= 10\) m/s²)

• Answer

GATE-CH-1990-13-i-mo-6mark

A mixture of coal and sand particles having sizes smaller than \(1 \times 10^{-4}\) m in diameter is to be separated by screening and subsequent elutriation with water.
(i) Recommend a screen aperture (\(\mu \)m) such that the oversize from the screen can be separated completely into sand and coal particles by elutriation.
(ii) Calculate also the required water velocity (mm/s).
Assume that Stokes’ law is applicable. Density of sand = 2650 kg/m\(^3\); density of coal = 1350 kg/m\(^3\); density of water = 1000 kg/m\(^3\); viscosity of water = \(1 \times 10^{-3}\) kg/m.s; g = 9.812 m/s\(^2\).
(i) ____________
{#1}

(ii) ____________
{#2}

GATE-CH-1995-16-mo-5mark

A binary mixture of 100 \(\mu \)m size having densities of 2 g/cm\(^3\) and 4 g/cm\(^3\) is to be classified by elutriation technique using water. Estimate the range [(i) minimum; (ii) maximum] of velocities (in mm/s) that can do the job and recommend a suitable value.
(i) ____________
{#1}

(ii) ____________
{#2}

GATE-CH-1995-2-k-mo-2mark

A suspension of uniform particles in water at a concentration of 500 kg of solids per cubic meter of slurry is settling in a tank. Density of the particles is 2500 kg/m\(^3\) and terminal velocity of a single particle is 20 cm/s. What will be the settling velocity of suspension? Richardson-Zaki index is 4.6

• 20 cm/s

• 14.3 cm/s

• 7.16 cm/s

• 3.58 cm/s

GATE-CH-1997-2-7-mo-2mark

A suspension of glass beads in ethylene glycol has a hindered settling velocity of 1.7 mm/s while the terminal settling velocity of the single glass bead in ethylene glycol is 17 mm/s. If the Richardson-Zaki hindered settling index is 4.5, the volume fraction of solids in the suspension is

• 0.1

• 0.4

• 0.6

• none of these

GATE-CH-2000-2-8-mo-2mark

A 30% (by volume) suspension of spherical sand particles in a viscous oil has a hindered settling velocity of 4.4 \(\mu \)m/s. If the Richardson-Zaki hindered settling index is 4.5, then the terminal settling velocity of sand grain is

• 0.9 \(\mu \)m/s

• 1 mm/s

• 22.1 \(\mu \)m/s

• 0.02 \(\mu \)m/s

GATE-CH-2005-56-mo-2mark

What is the terminal velocity in m/s, calculated from Stokes’ law, for a particulate of \(0.1\times 10^{-3}\) m, density 2800 kg/m³ settling in water of density 1000 kg/m³ and viscosity \(10^{-3}\) kg/(m.s)? (Assume \(g=10\) m/s²)

• \(2\times 10^{-2}\)

• \(4\times 10^{-3}\)

• \(10^{-2}\)

• \(8\times 10^{-3}\)

GATE-CH-2007-40-mo-2mark

In the Stokes’ regime, the terminal velocity of particles for centrifugal sedimentation is given by \[ v_t = \frac {\omega ^2 r(\rho _p - \rho )d_p^2}{18\mu } \] where, \(\omega \): angular velocity; \(r\): distance of the particle from the axis of rotation, \(\rho _p\): density of the particle; \(\rho \): density of the fluid; \(d_p\): diameter of the particle, and \(\mu \): viscosity of the fluid.
In a Bowl centrifugal classifier operating at 60 rpm with water (\(\mu =0.001\) kg.m^-1.s^-1), the time taken for a particle (\(d_p=0.0001\) m, sp.gr = 2.5) in seconds to traverse a distance of 0.05 m from the liquid surface is

• 4.8

• 5.8

• 6.8

• 7.8

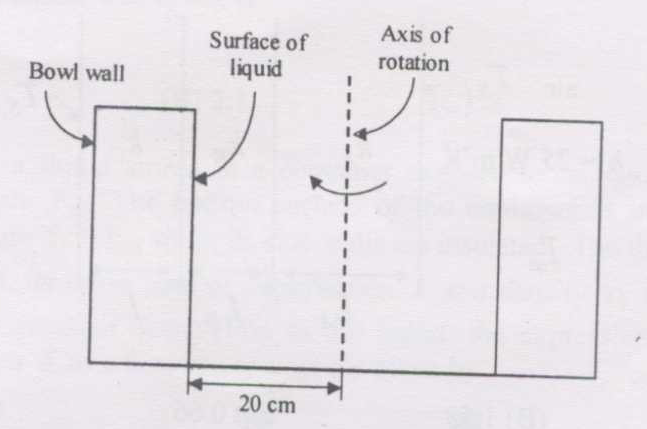
GATE-CH-2008-41-mo-2mark

Two identically sized spherical particles \(A\) and \(B\) having densities \(\rho _A\) and \(\rho _B\), respectively, are settling in a fluid of density \(\rho \). Assuming free settling under turbulent flow conditions, the ratio of the terminal settling velocity of particle \(A\) to that of particle \(B\) is given by

• \(\displaystyle \sqrt {\frac {\rho _A-\rho }{\rho _B-\rho }}\)

• \(\displaystyle \sqrt {\frac {\rho _B-\rho }{\rho _A-\rho }}\)

• \(\displaystyle \frac {\rho _A-\rho }{\rho _B-\rho }\)

• \(\displaystyle \frac {\rho _B-\rho }{\rho _A-\rho }\)

GATE-CH-2011-35-mo-2mark

The particle size distribution of the feed and collected solids (sampled for same duration) for a gas cyclone are given below:

Size range (µm)	1–5	5–10	10–15	15–20	20–25	25–30
Weight of feed  in the size range (g)	2	3	5	6	3	1
Weight of collected solids     in the size range (g)	0.1	0.7	3.6	5.5	2.9	1

What is the collection efficiency (in percentage) of the gas cyclone?

• 31

• 60

• 65

• 69

GATE-CH-1991-3-i-a-mo-2mark

Spherical particles of limestone (\(d_p\) = 0.16 mm, density = 2800 kg/m\(^3\)) take 5 minutes to settle under gravity through a 6 m column of a fluid of density 1200 kg/m\(^3\). The drag coefficient is equal to ––––-

• Answer

GATE-CH-1991-14-ii-mo-6mark

In a mixture of quartz (sp.gr = 2.65) and galena (sp.gr = 7.5), the size of the particles range from 0.0002 cm to 0.001 cm. On separation in a hydraulic classifier using water under free settling conditions, what are the size ranges of (i) quartz, and (ii) galena, in the pure products? (Viscosity of water = 0.001 kg/m.s; density = 1000 kg/m\(^3\)).
(i) pure quartz: 

(a) minimum size (\(\mu \)m)
{#1}

(b) maximum size (\(\mu \)m)
{#2}

(ii) pure galena: 

(a) minimum size (\(\mu \)m)
{#3}

(b) maximum size (\(\mu \)m)
{#4}

GATE-CH-1998-15-mo-5mark

A concentrated suspension of spherical quartz particles in water settles under gravity. The particle diameter is \(D_p = 10^{-5}\) m and the particle density is \(\rho _p\) = 2650 kg/m\(^3\). The initial voidage in the suspension is \(\epsilon = 0.8\).
Obtain the expression for the terminal velocity (\(v_t\)) of a single particle assuming Stokes’ law to be valid.
(a) Find the initial settling velocity (\(v_s\), in \(\mu \)m/s) of the particles in the suspension given \[ v_s = v_t \epsilon ^{4.6} \]
{#1}

(b) Calculate the upward velocity of water (in \(\mu \)m/s) in the suspension resulting from the settling of the particles for \(\epsilon = 0.8\).
{#2}