GATE-CH-2010-13-math-1mark

The Maxwell-Boltzmann velocity distribution for the \(x\)-component of the velocity at temperature \(T\), is \[ f(v_x) = \sqrt {\frac {m}{2\pi kT}}\exp \left (-\frac {mv_x^2}{2kT}\right ) \] The standard deviation of the distribution is

• \(\sqrt {2kT/m}\)

• \(kT/m\)

• \(\sqrt {kT/m}\)

• \(kT/2m\)

GATE-CH-2013-1-math-1mark

The number of emails received on six consecutive days is 11, 9, 18, 18, 4 and 15, respectively. What are the median and the mode for these data?

• 18 and 11, respectively

• 13 and 18, respectively

• 13 and 12.5, respectively

• 12.5 and 18, respectively

GATE-CH-2017-5-math-1mark

The marks obtained by a set of students are: \(38, 84, 45, 70, 75, 60, 48\). The mean and median marks, respectively, are:

• 45 and 75

• 55 and 48

• 60 and 60

• 60 and 70

GATE-CH-2007-28-math-2mark

The thickness of a conductive coating in micrometers has a probability density function of \(600x^{-2}\) for \(100 ?\mu \text {m} < x < 120 ?\mu \text {m}\). The mean and the variance of the coating thickness is

• 1 \(\mu \)m, 108.39 \(\mu \)m\(^2\)

• 33.83 \(\mu \)m, 1 \(\mu \)m\(^2\)

• 105 \(\mu \)m, 11 \(\mu \)m\(^2\)

• 109.39 \(\mu \)m, 33.83 \(\mu \)m\(^2\)

GATE-CH-2008-27-math-2mark

The normal distribution is given by \[ f(x) = \frac {1}{\sqrt {2\pi }\sigma }\exp \left (-\frac {(x-\mu )^2}{2\sigma ^2}\right ), \quad -\infty < x < \infty \] The points of inflexion to the normal curve are

• \(x=-\sigma , +\sigma \)

• \(x=\mu +\sigma , \mu -\sigma \)

• \(x=\mu +2\sigma , \mu -2\sigma \)

• \(x=\mu +3\sigma , ? \mu -3\sigma \)

GATE-CH-2008-30-math-2mark

The Poisson distribution is given by \(\displaystyle P(r) = \frac {m^r}{r!}\exp (-m)\). The first moment about the origin for this distribution is

• 0

• \(m\)

• \(1/m\)

• \(m^2\)

GATE-CH-2011-29-math-2mark

Fuel cell stacks are made of NINE membrane electrode assemblies (MEAs) interleaved between TEN bipolar plates (BPs) as illustrated below. The width of a membrane electrode assembly and a bipolar plate are normally distributed with \(\mu _{\text {MEA}}=0.15\), \(\sigma _{\text {MEA}}=0.01\), and \(\mu _{\text {BP}}=5\), \(\sigma _{\text {BP}}=0.1\) respectively. The widths of the different layers are independent of each other.

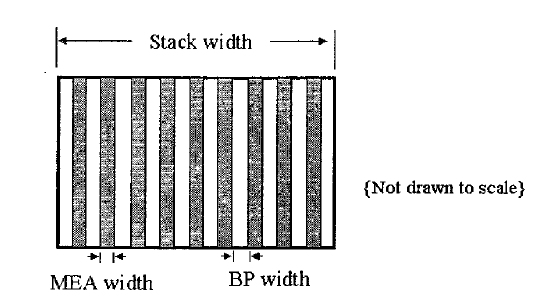
Which ONE of the following represents the CORRECT values of \((\mu _{\text {stack}}, \sigma _{\text {stack}})\) for the overall fuel cell stack width?

• \((51.35,0.32)\)

• \((51.35,1.09)\)

• \((5.15,0.10)\)

• \((5.15,0.11)\)

GATE-CH-2014-29-math-2mark

Consider the following two normal distributions 

\[ \begin{align*} f_1(x) &= \exp(-\pi x^2) \\ f_2(x) &= \frac{1}{2\pi}\exp\left\{-\frac{1}{4\pi}(x^2+2x+1)\right\} \end{align*} \]

If \(\mu \) and \(\sigma \) denote the mean and standard deviation, respectively, then

• \(\mu _1<\mu _2\) and \(\sigma _1^2<\sigma _2^2\)

• \(\mu _1<\mu _2\) and \(\sigma _1^2>\sigma _2^2\)

• \(\mu _1>\mu _2\) and \(\sigma _1^2<\sigma _2^2\)

• \(\mu _1>\mu _2\) and \(\sigma _1^2>\sigma _2^2\)

GATE-ME-2004-31-math-2mark

From a pack of regular from playing cards two cards are drawn random. What is the probability that both cards will be kings, if first card is NOT replaced?

• \(\dfrac {1}{26}\)

• \(\dfrac {1}{52}\)

• \(\dfrac {1}{169}\)

• \(\dfrac {1}{221}\)

GATE-ME-2013-A-24-math-1mark

Let \(X\) be a normal random variable with mean 1 and variance 4. The probability \(P\{X<0\}\) is

• 0.5

• Greater than 0 and less than 0.5

• Greater than 0.5 and less than 1.0

• 1.0