GATE-CH-1993-11-b-i-ht-1mark

Saturated steam is condensed as a film on a vertical plate of height 50 cm. If the local heat transfer coefficient at a distance of 50 cm from the top is 7200 W/m\(^2\).\(^\circ \)C, the average heat transfer coefficient over the entire plate in W/m\(^2\).\(^\circ \)C is

• 5400

• 7200

• 9600

• 14400

GATE-CH-1997-2-11-ht-2mark

For condensation of pure vapours, if the heat transfer coefficients in filmwise and dropwise condensation are respectively \(h_f\) and \(h_d\), then

• \(h_f = h_d\)

• \(h_f > h_d\)

• \(h_f < h_d\)

• \(h_f\) could be greater or smaller than \(h_d\)

GATE-CH-1999-1-13-ht-1mark

Gibbs phase rule finds application when heat transfer occurs by

• conduction

• convection

• radiation

• condensation

GATE-CH-2005-16-ht-1mark

In film type condensation of liquid along a vertical tube, the thickness of the condensate layer increases towards the bottom. This implies that the local heat transfer coefficient.

• increases from top to bottom

• decreases from top to bottom

• remains constant from top to bottom

• first increases and then decreases from top to bottom

GATE-CH-2011-18-ht-1mark

In film type condensation over a vertical tube, local heat transfer coefficient is

• inversely proportional to local film thickness

• directly proportional to local film thickness

• equal to local film thickness

• independent of local film thickness

GATE-CH-2016-10-ht-1mark

Steam at 100^oC is condensing on a vertical steel plate. The condensate flow is laminar. The average Nusselt numbers are \(\text {Nu}_1\) and \(\text {Nu}_2\), when the plate temperatures are 10^oC and 55^oC, respectively. Assume the physical properties of the fluid and steel to remain constant within the temperature range of interest. Using Nusselt equations for film-type condensation, what is the value of the ratio \(\text {Nu}_2/\text {Nu}_1\) ?

• 0.5

• 0.84

• 1.19

• 1.41

GATE-CH-2006-82-83-ht-4mark

In film condensation on a vertical plane surface, the \(x\) directional velocity distribution is given by \[ u(y) = \frac {g(\rho _l-\rho _v)}{\mu _l}\left (\delta y - \frac {1}{2}y^2\right ) \] where \(\delta \) is the film thickness at any \(x\).

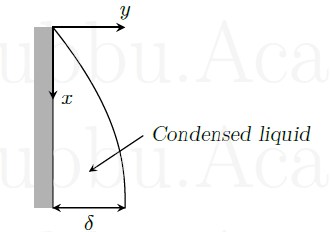
(i) The mass flow rate of the condensate \(m(x)\) through any axial position \(x\) per unit width of the plate is given by

{#1}

(ii) Differentiate \(m(x)\) with respect to \(\delta \) to get the differential increase in condensate mass \(dm\) with film thickness i.e., \(dm/d\delta \). Then obtain \(dm/dx\) assuming heat flux through the film to be due to conduction based on a linear temperature profile between the vapor and wall. Hence determine \(d\delta /dx\).
Here \(\mu _l\) is liquid viscosity, \(k_l\) is thermal conductivity, and \(\lambda \) is latent heat of condensation. \(T_v\) is the vapor temperature and \(T_w\) is the wall temperature.

{#2}

GATE-CH-2007-45-ht-2mark

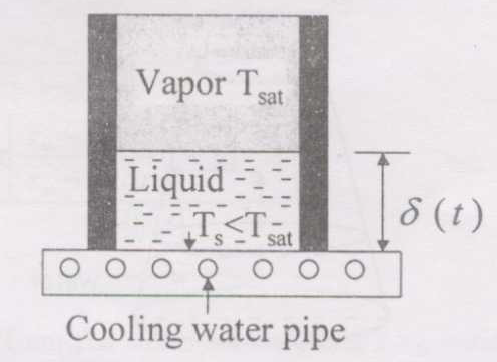
Consider a liquid stored in a container exposed to its saturated vapor at constant temperature \(T_{\text {sat}}\). The bottom surface of the container is maintained at a constant temperature \(T_s < T_{\text {sat}}\) while its side walls are insulated. The thermal conductivity \(k_l\) of the liquid, its latent heat of vapourisation \(\lambda \) and density \(\rho _l\) are known. Assuming a linear temperature distribution in the liquid, the expression for the growth of the liquid layer \(\delta \) as a function of time \(t\) is given by

• \({\displaystyle \delta (t) = \left [\frac {4k_l(T_{\text {sat}}-T_s)}{\rho _l\lambda }t\right ]^{1/2}}\)

• \({\displaystyle \delta (t) = \left [\frac {k_l(T_{\text {sat}}-T_s)}{2\rho _l\lambda }t\right ]^{1/2}}\)

• \({\displaystyle \delta (t) = \left [\frac {2k_l(T_{\text {sat}}-T_s)}{\rho _l\lambda }t\right ]^{1/2}}\)

• \({\displaystyle \delta (t) = \left [\frac {k_l(T_{\text {sat}}-T_s)}{\rho _l\lambda }t\right ]^{1/2}}\)

GATE-CH-1988-14-ii-ht-4mark

Condensing equipment may be mounted horizontally or vertically. For a laminar flow of condensate, derive an expression in \(D\), \(L\) and \(N\) that define the limiting tube length beyond which the condenser should be mounted horizontally for maximum value of heat transfer coefficient. \[ \text {Take: } \quad \frac {h_V}{h_H} = 1.56 \left (\frac {N^{2/3} D}{L}\right )^{1/4} \] where \(h_V\) and \(h_H\) are heat transfer coefficients for vertical and horizontal condenser respectively, \(N\) the number of tubes in vertical bank of tubes of diameter \(D\) and length \(L\).

• Answer

GATE-CH-1994-16-ht-5mark

Saturated steam at \(6.9 \times 10^4\) Pa pressure and 90\(^\circ \)C saturation temperature condenses on a vertical pipe of 0.025 m outside diameter and 0.3 m length. The average condensing heat transfer coefficient on the tube is 12000 W/m\(^2\).K. Other data:

Outside surface temperature of the pipe = 86\(^\circ \)C
Enthalpy of saturated steam = 2659 kJ/kg
Enthalpy of condensate = 375 kJ/kg
Viscosity of condensate at the film temperature = \(3.24 \times 10^{-4}\) Pa.s

Assume the flow of the condensate is laminar:

1. Calculate the rate of steam condensation
2. Check whether the flow is laminar.

• Answer