GATE-CH-1993-9-c-fm-2mark
1993-9-c-fm
Match the following: The shear stress vs. velocity gradient characteristics are shown in figure.
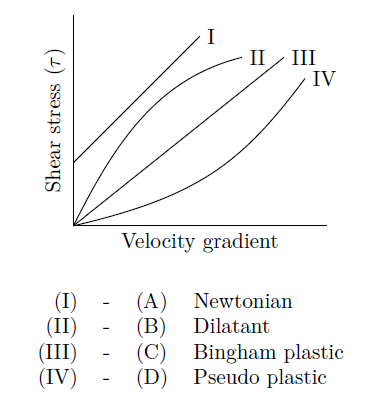
-
I.
-
II.
-
III.
-
IV.
1993-9-c-fm
Match the following: The shear stress vs. velocity gradient characteristics are shown in figure.

I.
II.
III.
IV.
1988-2-ii-fm
For pseudoplastic fluids, increase in shear rate
1989-2-i-c-fm
For a dilatant fluid, the magnitude of the slope of the shear stress versus the velocity gradient curve ––––- with increasing velocity gradient.
1994-1-j-fm
The shear stress–shear rate relationship for a liquid whose apparent viscosity decreases with increasing shear rate is given by
2001-2-6-fm
A Bingham fluid of viscosity ¥(¥mu ¥) = 10 Pa.s, and yield stress ¥(¥tau _o¥) = 10 kPa, is sheared between flat parallel plates separated by a distance 10¥(^{-3}¥) m. The top plate is moving with a velocity of 1 m/s. The shear stress on the plate is
2003-10-fm
A lubricant 100 times more viscous than water would have a viscosity (in Pa.s)
2004-49-fm
Viscosity of water at 40oC lies in the range of
2005-12-fm
Match the following types of fluid (in group I) with their respective constitutive relations (in group II), where ¥(¥tau ¥) is the stress and ¥(¥dot {¥gamma }¥) is the strain rate.
| Group I | Group II |
|---|---|
| (P) Pseudoplastic | (I) ¥(¥tau = ¥mu ¥dot {¥gamma }¥) |
| (Q) Bingham plastic | (II) ¥(¥tau = ¥tau _o + K¥dot {¥gamma }¥) |
| (III) ¥(¥tau = K|¥dot {¥gamma }|^n; ¥quad n < 1¥) | |
| (IV) ¥(¥tau = K|¥dot {¥gamma }|^n; ¥quad n > 1¥) |
2006-38-fm
A fluid obeying the constitutive equation ¥[ ¥tau = ¥tau _o + K ¥left (¥frac {dv_x}{dy}¥right )^{¥frac {1}{2}}, ¥quad ¥tau > ¥tau _o ¥] is held between two parallel plates a distance ¥(d¥) apart. If the stress applied to the top plate is ¥(3¥tau _o¥), then the velocity with which the top plate moves relative to the bottom plate would be
2013-10-fm
The apparent viscosity of a fluid is given by ¥(0.007 ¥left (¥dfrac {dV}{dy}¥right )^{0.3}¥) where ¥(¥left (¥dfrac {dV}{dy}¥right )¥) is the velocity gradient. The fluid is
2014-13-fm
Which of the following statements are CORRECT?
XE-2012-B-14-fm
The figure given below shows typical non-dimensional velocity profiles for fully developed laminar flow between two infinitely long parallel plates separated by a distance ¥(a¥) along ¥(y¥)-direction. The upper plate is moving with a constant velocity ¥(U¥) in the ¥(x¥)-direction and the lower plate is stationary.
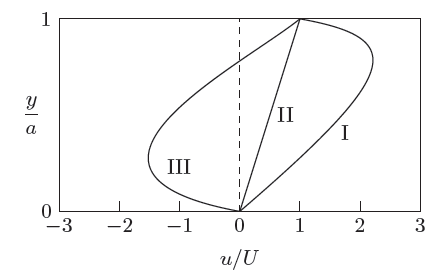
Match the non-dimensional velocity profiles in column I with the pressure gradients in column II.
| Column I | Column II |
|---|---|
| P. profile I | 1. ¥(¥dfrac {¥partial P}{¥partial x} > 0¥) |
| Q. profile II | 2. ¥(¥dfrac {¥partial P}{¥partial x} < 0¥) |
| R. profile III | 3. ¥(¥dfrac {¥partial P}{¥partial x} = 0¥) |
2012-52-53-fm
A Newtonian fluid of viscosity ¥(¥mu ¥) flows between two parallel plates due to the motion of the bottom plate (as shown below), which is moved with a velocity ¥(V¥). The top plate is stationary.
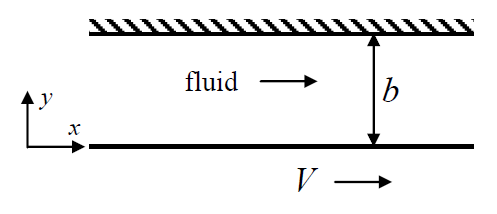
(i) The steady, laminar velocity profile in the ¥(x¥)-direction is
{#1}
(ii) The force per unit unit area (in the ¥(x¥)-direction) that must be exerted on the bottom plate to maintain the flow is
{#2}
Last Modified on: 02-May-2024
Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in