GATE-CH-1994-4-h-fm-1mark

For a sphere of density ${\rho }_s$ and volume $V$ placed in a fluid of density $\rho$

I. Weight {#1}

II. Buoyancy force {#2}

GATE-CH-2004-12-fm-1mark

What is the force required (in Newtons) to hold a spherical balloon stationary in water at a depth of $H$ from the air-water interface? The balloon is of radius 0.1 m and is filled with air.

• ${\displaystyle \frac{4\pi g}{3}}$

• ${\displaystyle \frac{0.1\pi gH}{4}}$

• ${\displaystyle \frac{0.1\pi gH}{8}}$

• ${\displaystyle \frac{0.04\pi gH}{3}}$

GATE-CH-2004-51-fm-2mark

A conical tank with a bottom opening of cross-sectional area $A$ is filled with water and is mounted on supports, as shown in the figure. What is the force $F$ with which plate $X$ must be pushed up to prevent water from leaking? Assume that the density of air is negligible as compared to the density of water ${\rho }_L$.

• ${\rho }_{L}Vg$

• ${\rho }_{L}AHg$

• ${\rho }_{L}Vg/2$

• ${\rho }_{L}Vg/3$

GATE-CH-2006-9-fm-1mark

The magnitude of the force (in N) required to hold a body of volume 0.05 m³ and mass 40 kg in water (density 1000 kg/m³) at a depth of 0.1 m is ($g=9.81$ m/s²)

• zero

• 98.1

• 490.5

• 882.9

GATE-CH-2007-10-fm-1mark

Consider a soap film bubble of diameter $D$. If the external pressure is $P_o$ and the surface tension of the soap film is $\sigma$, the expression for the pressure inside the bubble is

• $P_o$

• ${\displaystyle P_o+\frac{2\sigma }{D}}$

• ${\displaystyle P_o+\frac{4\sigma }{D}}$

• ${\displaystyle P_o+\frac{8\sigma }{D}}$

GATE-CH-2008-9-fm-1mark

Three containers are filled with water up to the same height as shown. The pressures at the bottom of the containers are denoted as $P_1,P_2$ and $P_3$. Which ONE of the following relationships is true?

• $P_3>P_1>P_2$

• $P_2>P_1>P_3$

• $P_1>P_2=P_3$

• $P_1=P_2=P_3$

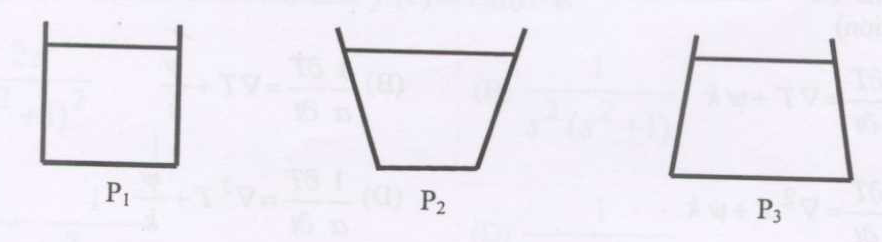
GATE-CH-2013-9-fm-1mark

An open tank contains two immiscible liquids of densities (800 kg/m³ and 1000 kg/m³) as shown in the figure. If $g=10$ m/s², under static conditions, the gauge pressure at the bottom of the tank in Pa is ____________

• Answer

GATE-CH-2016-8-fm-1mark

A vertical cylindrical vessel has a layer of kerosene (of density 800 kg/m³) over a layer of water (of density 1000 kg/m³). L-shaped glass tubes are connected to the column 30 cm apart. The interface between the two layers lies between the two points at which the L-tubes are connected. The levels (in cm) to which the liquids rise in the respective tubes are shown in the figure below.

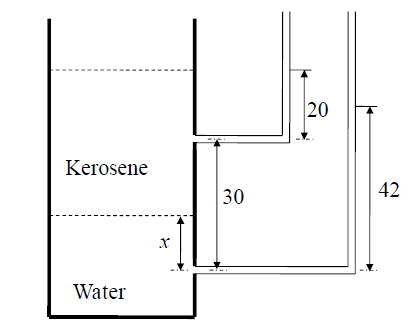
The distance ($x$ in cm, rounded off to the first decimal place) of the interface from the point at which the lower L-tube is connected is ____________

• Answer

GATE-CH-1989-12-i-fm-4mark

A jar is filled with two immiscible fluids $A$ and $B$ of densities 2000 kg/m${}^3$ and 1000 kg/m${}^3$. A ball of 4 $\times {10}^{-6}$ m${}^3$ volume and 0.01 kg mass is held submerged successively (a) in phase $A$ (b) exactly at the interface of $A$ and $B$, and (c) in phase $B$. Calculate the magnitude of the force (in N, correct to four decimals) required to hold the ball in position for each of the above cases.
 

(a) {#1}

(b) {#2}

(c) {#3}

GATE-CH-2005-82-fm-4mark

A balloon of mass 0.01 kg is charged with hydrogen to a pressure of 102 kPa and released from the ground level. During its rise the hydrogen is permitted to escape from the balloon in order to maintain a constant differential pressure of 2 kPa under which condition the diameter of the balloon remains at 0.4 m. As this balloon rises it is assumed that the temperature in and around the balloon remains constant at 273 K. Further, the inertia of the balloon and the air resistance due to rising balloon may be neglected. Assume that the density of air at 273 K is 1.2733 kg/m³, the average molecular weight of air is 28.9, the atmospheric pressure is 100 kPa and the acceleration due to gravity is 10 m/s².

(i) Select the correct value of the upward thrust (in N) expressed in terms of the outside pressure $P$ which is expressed in Pa.

{#1}

(ii) Select the value of the outside pressure $P$ in Pa for which there will be no force on the balloon?

{#2}

GATE-CH-2004-50-fm-2mark

For the manometer setup shown in the figure, the pressure difference $P_A-P_B$ is given by

• $({\rho }_H-{\rho }_{\text{air}})gH$

• $({\rho }_H-{\rho }_L)gH$

• $({\rho }_H-{\rho }_L)gH+({\rho }_L-{\rho }_{\text{air}})g(L-H)$

• $({\rho }_H-{\rho }_L)gL+({\rho }_L-{\rho }_{\text{air}})gH$

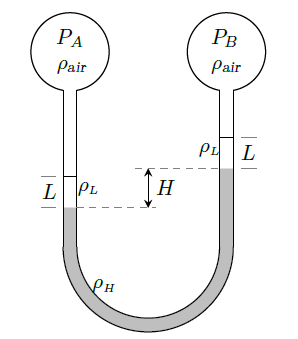
GATE-CH-2005-51-fm-2mark

A dam of width 50 m is used to hold water in a reservoir. If the water height is 10 m from the bottom of the dam, what is the total force $F$ acting on the dam due to the water? Assume $g=10$ m/s², and the fluid density is 1000 kg/m³.

• $F=12.5\times {10}^6$ N

• $F=25\times {10}^6$ N

• $F=50\times {10}^6$ N

• $F=5\times {10}^6$ N

GATE-CH-2005-52-fm-2mark

The relation between the stress $\tau$ and the strain rate $(d{u}_x/dy)$ for the rapid flow of a granular material is given by $$\tau =B{\left(\frac{d{u}_x}{dy}\right)}^2$$ where $B$ is a constant. If M, L and T are the mass, length and time dimension respectively, what is the dimension of the constant $B$?

• ML${}^{-1}$T${}^{-1}$

• ML${}^{-1}$T${}^{-2}$

• MT${}^{-1}$

• ML${}^{-1}$

GATE-CH-2010-34-fm-2mark

A hydrometer, with stem cross-sectional area of $2.82\times {10}^{-5}$ m², is immersed in a very large vessel containing water as shown in the figure. The immersed volume is $15\times {10}^{-6}$ m³ and the length of the stem above water surface is $L_w$. If the entire volume of water is replaced by a liquid with specific gravity 1.5 and if the length of the stem above the liquid surface is $L_l$, then the difference, $L_l-L_w$, is

• $-177$ mm

• 177 mm

• $-266$ mm

• 266 mm

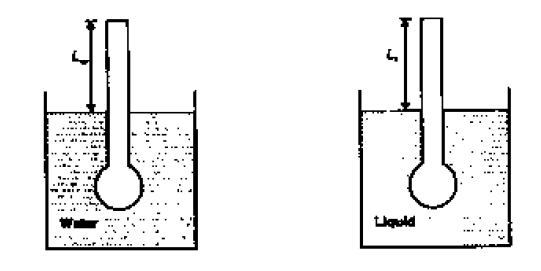
GATE-CH-1990-12-ii-fm-6mark

Water flowing at 1.5 litre/s in a 0.05 m diameter tube is measured by means of a simple orifice of diameter 0.025 m. If the coefficient of discharge is 0.62, what will be the reading (in cm) on a mercury-under-water manometer connected to the meter? Density of water = 1000 kg/m${}^3$; Viscosity of water = 0.001 N.s/m${}^2$; Density of mercury = 13,600 kg/m${}^3$.
____________

• Answer

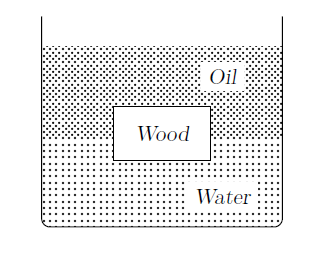
GATE-CH-1993-19-b-fm-5mark

A piece of wood floats at the interface between layers of oil and water as shown in figure. The specific gravity of wood and oil are 0.95 and 0.75 respectively. Determine the volume fraction of wood in the water layer.
____________

• Answer

GATE-CH-1997-15-fm-5mark

A rectangular piece of wood (density = 650 kg/m${}^3$) 75 mm $\times$ 75 mm $\times$ 2000 mm in size floats on water (density = 1000 kg/m${}^3$). How many kilograms of lead of density 11,200 kg/m${}^3$ must be put on the top of the wooden piece so that it will float upright with 300 mm of its length above the water surface?
____________

• Answer

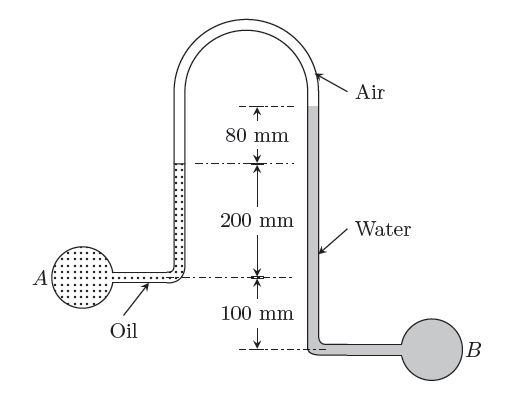
GATE-ME-2016-S1-39-fm-2mark

An inverted U-tube manometer is used to measure the pressure difference between two pipes $A$ and $B$, as shown in the figure. Pipe $A$ is carrying oil (specific gravity = 0.8) and pipe $B$ is carrying water. The densities of air and water are 1.16 kg/m³ and 1000 kg/m³, respectively. The pressure difference between pipes $A$ and $B$ is ____________kPa. Acceleration due to gravity $g=10$ m/s².

• Answer