0300-2-fm-1mark

Indicate what will be the manometric reading if the venturi meter is replaced by an orifice meter of the same size:

• less than that for venturi meter

• same as that for venturi meter

• higher than that for venturi meter

GATE-CH-1994-2-i-fm-1mark

For an orifice meter, the pressure recovery is ––––- than that for a venturi meter.

• less

• more

GATE-CH-1995-2-m-fm-2mark

A Pitot tube indicates 5 cm of water (manometer) when it is being used for measuring velocity of air. The velocity of air in m/s is

• 5

• 14.1

• 56.22

• 28.2

GATE-CH-1996-2-4-fm-2mark

A rotameter, through which air at room temperature and atmospheric pressure is flowing, gives a certain reading for a flow rate of 100 cc/s. If helium (Molecular weight 4) is used and the rotameter shows the same reading, the flow rate is

• 26 cc/s

• 42 cc/s

• 269 cc/s

• 325 cc/s

GATE-CH-2001-1-7-fm-1mark

The operation of a rotameter is based on

• variable flow area

• rotation of a turbine

• pressure drop across a nozzle

• pressure at a stagnation point

GATE-CH-2011-23-fm-1mark

In an orifice meter, if the pressure drop across the orifice is overestimated by 5%, then the PERCENTAGE error in the measured flow rate is

• \(+2.47\)

• \(+5\)

• \(-2.47\)

• \(-5\)

GATE-CH-2012-11-fm-1mark

The local velocity of a fluid along a streamline can be measured by

• Pitot tube

• Venturi meter

• Rotameter

• Orifice meter

GATE-IN-2013-18-fm-1mark

The differential pressure transmitter of a flow meter using a venturi tube reads \(2.5\times 10^5\) Pa for a flow rate of 0.5 m³/s. The approximate flow rate in m³/s for a differential pressure \(0.9\times 10^5\) Pa is

• 0.30

• 0.18

• 0.83

• 0.60

GATE-CH-1987-12-iv-fm-2mark

A liquid of specific gravity 1.25 is draining from the bottom of a large open tank through a 50 mm ID pipe. The drain pipe ends at a position 5 m below the surface of the liquid in the tank. Calculate the velocity of flow (in m/s) at the point of discharge from the pipe. Explain the significance of the result.
____________

• Answer

GATE-CH-2014-50-fm-2mark

In a steady and incompressible flow of a fluid (density = 1.25 kg/m³), the difference between stagnation and static pressures at the same location in the flow is 30 mm of mercury (density = 13600 kg/m³). Considering gravitational acceleration as 10 m/s², the fluid speed (in m/s) is ____________

• Answer

GATE-CH-1999-9-fm-5mark

Flow rate of water flowing through a pipe is being measured by using an orifice meter as shown in the figure.

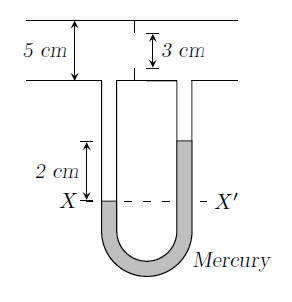
1. What is the direction of flow in the pipe?
{#1}
2. Derive an expression for velocity through the orifice. Determine the flow rate (ltr/s) for an orifice coefficient of 0.8
{#2}

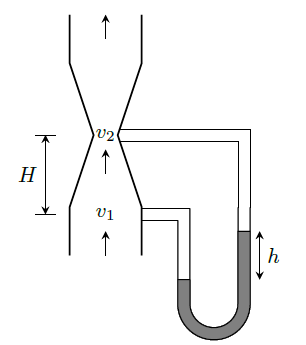
GATE-CH-2003-75-fm-2mark

The pressure differential across a vertical venturi meter (shown in figure) is measured with the help of a mercury manometer to estimate flow rate of water flowing through it. The expression for the velocity of water at the throat is

• \(\displaystyle \frac {v_2^2-v_1^2}{2g} = \frac {h\rho _m}{\rho _f}\)

• \(\displaystyle \frac {v_2^2-v_1^2}{2g} = \frac {h(\rho _m-\rho _w)}{\rho _f}\)

• \(\displaystyle \frac {v_2^2-v_1^2}{2g} = H + \frac {h(\rho _m-\rho _w)}{\rho _f}\)

• \(\displaystyle \frac {v_2^2}{2g} = \frac {h(\rho _m-\rho _w)}{\rho _f}\)

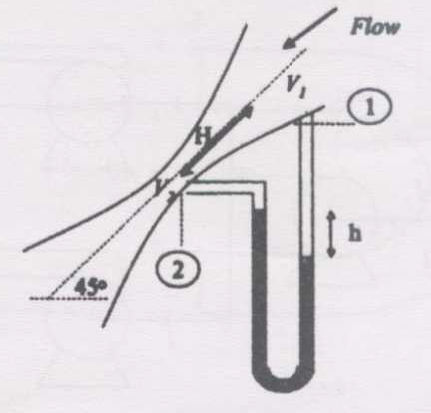
GATE-CH-2007-39-fm-2mark

The pressure differential across a venturi meter, inclined at 45^o to the vertical (as shown in the figure) is measured with the help of a manometer to estimate the flowrate of a fluid flowing through it. If the density of the flowing fluid is \(\rho \) and the density of the manometer fluid is \(\rho _m\), the velocity of the fluid at the throat can be obtained from the expression

• \(\displaystyle \frac {v_2^2-v_1^2}{2g} = \frac {h(\rho _m-\rho )}{\rho } + H\sin 45^{\circ }\)

• \(\displaystyle \frac {v_2^2-v_1^2}{2g} = \frac {h\rho _m}{\rho } + H\sin 45^{\circ }\)

• \(\displaystyle \frac {v_2^2-v_1^2}{2g} = \frac {h\rho _m}{\rho }\)

• \(\displaystyle \frac {v_2^2-v_1^2}{2g} = \frac {h(\rho _m-\rho )}{\rho }\)

GATE-CE-2018-S2-34-fm-2mark

In a 5 m wide rectangular channel, the velocity \(u\) distribution in the vertical direction \(y\) is given by \(u=1.25y^{1/6}\). The distance \(y\) is measured from the channel bed. If the flow depth is 2 m, the discharge per unit width of the channel is

• 2.40 m³/s/m

• 2.80 m³/s/m

• 3.27 m³/s/m

• 12.02 m³/s/m

GATE-CH-1987-12-ii-fm-2mark

Air is flowing in a 50 mm ID tube. There is a venturi meter in the line, and the manometric fluid is water. Calculate the volumetric flow rate of air (in m\(^3\)/s) for the following conditions:

Manometric reading = 100 mm water
Density of water = 1000 kg/m\(^3\)
Density of air = 1.185 kg/m\(^3\)
Coefficient of discharge = 0.98
Diameter of venturi throat = 25 mm
Pressure of air = 1 atm.

____________

• Answer

GATE-CH-1991-13-i-fm-4mark

What diameter of orifice (in mm) would give a pressure difference of 41 cm water column for the flow of liquid styrene of specific gravity 0.9 at 0.055 m\(^3\)/s in a 250 mm diameter pipe? Assume \(C_d = 0.62\)
____________

• Answer

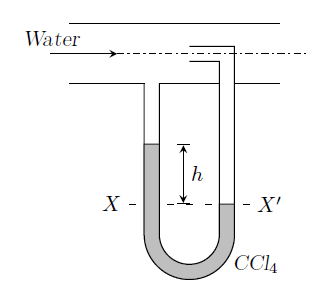
GATE-CH-1993-19-a-fm-5mark

Water flows through a 30 mm i.d. pipe at atmospheric pressure. The velocity of water at the center of the pipe is measured by a Pitot tube as shown in Figure. The pressure difference between the impact tube and the static tube is 20 cm of Carbon tetra chloride (density = 1600 kg/m\(^3\)). Calculate the volumetric flow rate through the pipe in cubic meter per hour. Viscosity of water is 1 cP.
____________

• Answer