GATE-CH-1988-2-v-fm-1mark

For a fluidized bed, with the increase in expansion of the bed, up to solids carry over from the bed, the pressure drop across the bed

• increases rapidly

• decreases rapidly

• first increases then decreases

• remains essentially constant

GATE-CH-1992-3-b-fm-2mark

A spherical particle is falling slowly in a viscous liquid such that Reynolds number is less than 1. Which statement is correct for this situation?

• Inertial and drag forces are important

• Drag, gravitational and buoyancy forces are important

• Drag force and gravitational forces are important

• None of the above

GATE-CH-1992-3-c-fm-2mark

As the velocity \(V\) and thus the Reynolds number of a flow past a sphere increases from very low values, the drag force for \(\text {Re} \ll 1\)

• Increases linearly with \(V\)

• Decreases linearly with \(V\)

• Decreases as \(V^2\)

• None of these

GATE-CH-1993-9-b-fm-2mark

In fluidization using perfect spherical particles the operating range of fluidization velocity is

• independent of particle size

• greater for bigger particle size

• greater for smaller particle size

• proportional to the square of particle size

GATE-CH-1995-1-e-fm-1mark

A particle attains its terminal settling velocity when

• gravity force + drag force = buoyancy force

• buoyancy force + drag force = gravity force

• drag force = buoyancy force

GATE-CH-1995-2-i-fm-2mark

Hydraulic mean diameter for flow through packed bed of spherical particles of size \(D_p\) with porosity \(\epsilon \) is

• \(\displaystyle D_p \frac {1}{6}\frac {\epsilon }{1-\epsilon }\)

• \(\displaystyle D_p \frac {1}{6}\frac {1-\epsilon }{\epsilon }\)

• \(\displaystyle D_p \frac {2}{3}\frac {1-\epsilon }{\epsilon }\)

• \(\displaystyle D_p \frac {2}{3}\frac {\epsilon }{1-\epsilon }\)

GATE-CH-1995-2-l-fm-2mark

Bed pressure drop in an air fluidised bed of catalyst particles (\(\rho _p\) = 2000 kg/m\(^3\), \(D_p\) = 0.05 cm) of 60 cm bed depth and bed porosity of 0.5, expressed in cm of water (manometer) is

• 90

• 60

• 45

• 30

GATE-CH-1997-1-8-fm-1mark

In the low Reynolds number region, the drag force on a sphere is proportional to (where \(v\) is the terminal settling velocity of the sphere in a viscous medium)

• \(v\)

• \(v^2\)

• \(v^4\)

• \(v^{0.5}\)

GATE-CH-1997-2-6-fm-2mark

For laminar flow of a fluid through a packed bed of spheres of diameter \(D\), the pressure drop per unit length of bed depends upon the sphere diameter as

• \(D\)

• \(D^2\)

• \(D^4\)

• \(1/D^2\)

GATE-CH-2002-2-3-fm-2mark

The drag coefficient for a bacterium moving in water at 1 mm/s, will be of the following order of magnitude (assume size of the bacterium to be 1 micron and kinematic viscosity of water to be \(10^{-6}\) m²/s)

• 24000

• 24

• 0.24

• 0.44

GATE-CH-2004-55-fm-2mark

\(U_{\text {mf}}\) is the minimum fluidization velocity for a bed of particles. An increase in the superficial gas velocity from \(2U_{\text {mf}}\) to \(2.5U_{\text {mf}}\) results in (all velocities are smaller than the entrainment velocity of the particles) no change in

• drag on particles

• drag on column walls

• the bed height

• the bed voidage

GATE-CH-2004-56-fm-2mark

The Kozeny-Carman equation, rewritten in terms of non-dimensional numbers, gives \((\Delta P/\rho v^2)\) proportional to

• \(\displaystyle \frac {(L/D_P)}{\text{Re} }\)

• \(\displaystyle \frac {\text{Re} }{(D_P/L)}\)

• \(\displaystyle \frac {(L/D_P)}{\text{Re} ^2}\)

• \(\displaystyle \frac {\text{Re} ^2}{(D_P/L)}\)

GATE-CH-2009-32-fm-2mark

The terminal settling velocity of a 6 mm diameter glass sphere (density: 2500 kg/m³) in a viscous Newtonian fluid (density: 1500 kg/m³) is 100 \(\mu \)m/s. If the particle Reynolds number is small and the value of acceleration due to gravity is 9.81 m/s², then the viscosity of the liquid (in Pa.s) is

• 100

• 196.2

• 245.3

• 490.5

GATE-CH-2009-7-fm-1mark

Under fully turbulent flow conditions, the frictional pressure drop across a packed bed varies with the superficial velocity (\(v\)) of the fluid as

• \(v^{-1}\)

• \(v\)

• \(v^{3/2}\)

• \(v^2\)

GATE-CH-2010-20-fm-1mark

The height of a fluidized bed at incipient fluidization is 0.075 m, and the corresponding voidage \(0.38\). If the voidage of the bed increases to \(0.5\), then the bed height would be

• 0.058 m

• 0.061 m

• 0.075 m

• 0.093 m

GATE-CH-2011-15-fm-1mark

Consider the following two cases of movement of particles. In Case I, the particles moves along the positive \(y\)-direction and in Case II, the particles moves along negative \(y\)-direction. Gravity acts along the positive \(y\)-direction. Which ONE of the following options corresponds to the CORRECT directions of buoyancy acting on the particles?

• Positive \(y\)-direction for both the cases

• Negative \(y\)-direction for Case I, positive \(y\)-direction for Case II

• Negative \(y\)-direction for both the cases

• Positive \(y\)-direction for Case I, negative \(y\)-direction for Case II

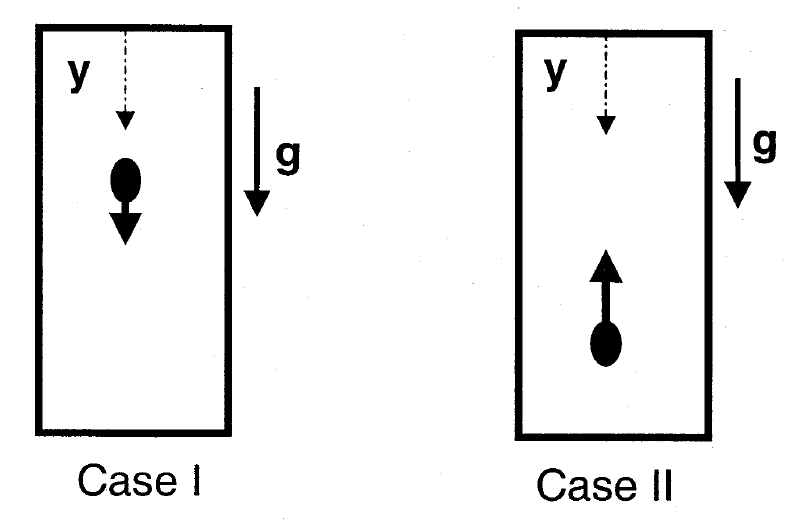
GATE-CH-2015-34-fm-2mark

For Fanning friction factor \(f\) (for flow in pipes) and drag coefficient \(C_D\) (for flow over immersed bodies), which of the following statements are true?

• [P:] \(f\) accounts only for the skin friction
• [Q:] \(C_D\) accounts only for the form friction
• [R:] \(C_D\) accounts for both skin and form friction
• [S:] Both \(f\) and \(C_D\) depend on the Reynolds number
• [T:] For laminar flow through a pipe, \(f\) doubles on doubling the volumetric flow rate

• R, S, T

• P, Q, S

• P, R, S

• P, Q, S, T

GATE-CH-1990-2-iv-fm-2mark

The pressure drop required for fluidizing a coal bed with a liquid petroleum fraction of viscosity 0.015 N.s/m\(^2\) is \(10^5\) N/m\(^2\). The pressure drop required for fluidizing the same bed with an oil of viscosity 0.03 N.s/m\(^2\) is ____________\(\times 10^5\) N/m\(^2\)

• Answer

GATE-CH-1990-3-iv-fm-2mark

To increase the capacity of a commercial packed bed adsorber, the volumetric flow rate of gas entering is increased by 20 percent. The ratio of pressure drops (new to old) is ____________

• Answer

GATE-CH-2015-12-fm-1mark

A cylindrical packed bed of height 1 m is filled with equal sized spherical particles. The particles are nonporous and have a density of 1500 kg/m³. The void fraction of the bed is 0.45. The bed is fluidized using air (density 1 kg/m³). If the acceleration due to gravity is 9.8 m/s², the pressure drop (in Pa) across the bed at incipient fluidization (up to one decimal place) is ____________

• Answer

GATE-CH-2017-11-fm-1mark

A gas bubble (gas density \(\rho _g = 2\) kg/m³; bubble diameter \(D=10^{-4}\) m) is rising vertically through water (density \(\rho =1000\) kg/m³; viscosity \(\mu =0.001\) Pa.s). Force balance on the bubble leads to the following equation, \[ \frac {dv}{dt} = -g\frac {\rho _g-\rho }{\rho _g}-\frac {18\mu }{\rho _g D^2}v \] where \(v\) is the velocity of the bubble at any given time \(t\). Assume that the volume of the rising bubble does not change. The value of \(g=9.81\) m/s ².

The terminal rising velocity of the bubble (in cm/s), rounded to 2 decimal places, is ____________

• Answer

GATE-CH-2003-53-54-fm-4mark

A bed of spherical particles (sp. gravity 2.5) of uniform size 1500 \(\mu \)m is 0.5 m in diameter and 0.5 m high. In the packed bed state, the porosity may be taken as 0.4. Ergun’s equation for the above particle-fluid system (in SI units) is given below \[ \Delta P/L = 375 \times 10^3 v_{om} + 10.94 \times 10^6 v_{om}^2 \quad \quad \text {(SI units)} \] (i) If water is to be used as the fluidizing medium, the minimum fluidization velocity, \(v_{om}\) is

{#1}

(ii) In actual operation, the above bed has a height = 1 m. What is the porosity of the fluidized bed?

{#2}

GATE-CH-2007-84-85-fm-4mark

A fluidized bed (0.5 m dia, 0.5 m high) of spherical particles (diameter = 2000 \(\mu \)m, specific gravity = 2.5) uses water as the medium. The porosity of the bed is 0.4. The Ergun equation for the system is \[ \Delta P/L = 4 \times 10^5 U_{mf} + 1 \times 10^7 U_{mf}^2 \] (SI unit, \(U_{mf}\) in m/s; \(g=9.8\) m/s²)

(i) \(\Delta P/L\) (SI unit) at the minimum fluidization condition is

{#1}

(ii) The minimum fluidization velocity (mm/s) is

{#2}

GATE-CH-2011-48-49-fm-4mark

For a liquid flowing through a packed bed, the pressure drop per unit length of bed \(\Delta P/L\) is \[ \frac {\Delta P}{L} = \frac {150\mu _f V_0(1-\varepsilon )^2}{(\phi _s\bar {d_p})^2 \varepsilon ^3} + \frac {1.75\rho _f v_0^2(1-\varepsilon )}{\phi _s\bar {d_p}\varepsilon ^3} \] where \(v_0\) is the superficial liquid velocity, \(\varepsilon \) is the bed porosity, \(\bar {d_p}\) is the average particle size, \(\phi _s\) is particle sphericity, \(\rho _f\) is liquid density and \(\mu _f\) is liquid viscosity.
Given data: \(\bar {d_p} = 1\times 10^{-3}\) m, \(\phi _s=0.8, \rho _f = 1000\) kg/m³, \(\mu _f=1\times 10^{-3}\) kg.m^-1.s^-1, particle density, \(\rho _p=2500\) kg/m³ and acceleration due to gravity, \(g=9.8\) m/s².

(i) When \(v_0\) is 0.005 m/s and \(\varepsilon =0.5\), which ONE of the following is CORRECT value for the ratio of viscous loss to the kinetic energy loss?

{#1}

(ii) On further increasing \(v_0\), incipient fluidization is achieved. Assuming that the porosity of the bed remains unaltered, the pressure drop per unit length (in Pa/m) under incipient fluidization condition is

{#2}

GATE-CH-2002-2-4-fm-2mark

A gas (density = 1.5 kg/m³, viscosity = \(2\times 10^{-5}\) kg/m.s) flowing through a packed bed (particle size = 0.5 cm, porosity = 0.5) at a superficial velocity of 2 m/s causes a pressure drop of 8400 Pa/m. The pressure drop for another gas, with density of 1.5 kg/m³ and viscosity of \(3\times 10^{-5}\) kg/m.s, flowing at 3 m/s will be

• 8400 Pa/m

• 18900 Pa/m

• 12600 Pa/m

• 16800 Pa/m

GATE-CH-2006-39-fm-2mark

A bed fluidized by water is used for cleaning sand contaminated with salt. The particles of sand and salt have the same shape and size but different densities (\(\rho _{\text {sand}} = 2500\) kg/m³ and \(\rho _{\text {salt}} = 2000\) kg/m³). If the initial volume fraction of the salt in the mixture is 0.3 and if the value of the minimum fluidization velocity (\(U_{\text {mf}}\)) is 0.9 m/s, find the final value of the \(U_{\text {mf}}\) (in m/s) when the sand is washed free of the salt. Assume that the bed characteristics (bed porosity and solid surface area per unit volume) do not change during the operation and that the pressure drop per unit length is directly proportional to the fluid velocity.

• 0.70

• 0.90

• 1.00

• 1.46

GATE-CH-2006-40-fm-2mark

Two spherical particles have the same outer diameter but are made of different materials. The first one (with material density \(\rho _1\)) is solid, whereas the second (with material density \(\rho _2\)) is a hollow sphere with the inner shell diameter equal to half the outer diameter. If both the spheres have the same terminal velocity in any fluid, then the ratio of their material densities, \(\rho _2/\rho _1\), is

• 1

• 8/7

• 2

• 8

GATE-CH-2010-35-fm-2mark

The diameter of a drop of liquid fuel changes with time, due to combustion, according to the relationship, \(\displaystyle D=D_o\left (1-\frac {t}{t_b}\right )\). While burning, the drop falls at its terminal velocity under Stokes flow regime. The distance it will travel before complete combustion, is given by

• \(\displaystyle \frac {D_o^2\Delta \rho t_b g}{18\mu }\)

• \(\displaystyle \frac {D_o^2\Delta \rho t_b g}{36\mu }\)

• \(\displaystyle \frac {D_o^2\Delta \rho t_b g}{54\mu }\)

• \(\displaystyle \frac {D_o^2\Delta \rho t_b g}{108\mu }\)

GATE-CH-2012-32-fm-2mark

A bed of spherical glass beads (density 3000 kg/m³, diameter 1 mm, bed porosity 0.5) is to be fluidized by a liquid of density 1000 kg/m³ and viscosity 0.1 Pa.s. Assume that the Reynolds number based on particle diameter is very small compared to one. If \(g=10\) m/s², then the minimum velocity (in m/s) required to fluidize the bed is

• \(3.33\times 10^{-4}\)

• \(3.33\times 10^{-1}\)

• 3

• 30

GATE-XE-2012-B-15-fm-2mark

Air flows over a spherical storage vessel of diameter 4 m at a speed of 1 m/s. To find the drag force on the vessel, a test run is to be carried out in water using a sphere of diameter 100 mm. The density and dynamic viscosity of air are 1.2 kg/m³ and \(1.8\times 10^{-5}\) Pa.s, respectively. The density and dynamic viscosity of water are 1000 kg/m³ and \(10^{-3}\) Pa.s, respectively. The drag force on the model is 4 N under dynamically similar conditions. The drag force (in N) on the prototype is approximately

• 0.25

• 0.93

• 1.08

• 4

GATE-CH-1994-13-fm-5mark

A tube of 0.05 m\(^2\) cross-sectional area is packed with spherical particles up to a height of 0.25 m. The porosity of the bed is 0.35. It is desired to fluidize the particles with water (\(\rho \) = 1000 kg/m\(^3\), \(\mu \) = 10\(^{-3}\) Pa.s). Calculate the minimum fluidization velocity (in cm/s) of fluidization given the Ergun’s equation: \[ \frac {\Delta P}{\rho } = \frac {1.75v^2 L(1-\varepsilon )}{D_p \varepsilon ^3} + \frac {150 \mu v (1-\varepsilon )^2}{D_p^2 \varepsilon ^3}\frac {L}{\rho } \] Data:
Diameter of particles = 0.01 m; Density of solid particles = 2600 kg/m\(^3\).
____________

• Answer

GATE-CH-1995-18-fm-5mark

Air flows through a packed bed of a powdery material of 1 cm depth at a superficial gas velocity of 1 cm/s. A manometer connected to the unit registers a pressure drop of 1 cm of water. The bed has a porosity of 0.4. Assuming that Kozeny-Carman equation is valid for the range of study, estimate the particle size of the powder (in mm).
\(\rho _{\text {air}}\) = 1.23 kg/m\(^3\); \(\mu _{\text {air}} = 1.8 \times 10^{-5}\) kg/(m.s).
____________

• Answer

GATE-CH-1996-13-fm-5mark

Water trickles by gravity over a bed of particles, each 1 mm dia in a bed of dia 6 cm and height 2 m. The water is fed from a reservoir whose diameter is much larger than that of the packed bed, with water maintained at a height of 0.1 m above the top of the bed. The bed has a porosity of 0.31. Calculate the volumetric flow rate (in cm\(^3\)/s) of water if its viscosity is 1.0 cP and density is 1000 kg/m\(^3\).
____________

• Answer

GATE-CH-2015-37-fm-2mark

A spherical solid particle of 1 mm diameter is falling with a downward velocity of 1.7 mm/s through a liquid (viscosity 0.04 Pa.s) at a low Reynolds number (Stokes regime). The liquid is flowing upward at a velocity of 1 mm/s. All velocities are with respect to a stationary reference frame.

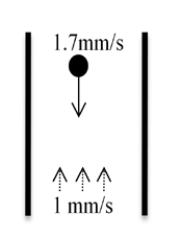
Neglecting the wall effects, the drag force per unit projected area of the particle, in Pa, (up to two decimal places) is ____________

• Answer

GATE-CH-2016-37-fm-2mark

Consider a rigid solid sphere falling with a constant velocity in a fluid. The following data are known at the conditions of interest: viscosity of the fluid = 0.1 Pa.s, acceleration due to gravity = 10 m/s², density of the particle = 1180 kg/m ³ and density of the fluid = 1000 kg/m³. The diameter (in mm, rounded off to the second decimal place) of the largest sphere that settles in the Stokes’ law regime (Reynolds number \(\le 0.1\)), is ____________

• Answer