GATE-CH-1989-8-i-a-ctrl-2mark

Oscillations of a system may be reduced by one of the following controllers [[1]] for one of the following reasons [[2]].

GATE-CH-1989-8-i-b-ctrl-2mark

The response of a first order system with a proportional controller Kc has an offset to a step input. The offset can be eliminated by which one of the following actions? [[1]] By this action, what happens to the overall order of the system? [[2]]

GATE-CH-1991-9-iv-ctrl-2mark

The type of process that most often can benefit from derivative control is:

• Flow

• Level

• Temperature

• Pressure

GATE-CH-1996-2-15-ctrl-2mark

The transfer function for an ideal proportional plus reset controller (Reset time \(\tau \)) is

• \(\displaystyle K_{c}\left (1 + \frac {1}{\tau s}\right )\)

• \(K_{c}(1 + \tau s)\)

• \(\dfrac {K_{c}}{1 + \tau s}\)

• \(\dfrac {K_{c}}{1 + \dfrac {s}{\tau }}\)

GATE-CH-1997-1-23-ctrl-1mark

The transfer function of a PID controller is

• \(K_c(1+\tau _Is+\tau _Ds)\)

• \(\displaystyle K_c\left (1+\frac {1}{\tau _Is}+\tau _Ds\right )\)

• \(\displaystyle K_c\left (1+\tau _Is+\frac {1}{\tau _Ds}\right )\)

• \(\displaystyle K_c\left (1+\frac {1}{\tau _Is} + \frac {1}{\tau _Ds}\right )\)

GATE-CH-1997-1-27-ctrl-1mark

A proportional controller with a gain of \(K_c\) is used to control a first-order process. The offset will increase if

• \(K_c\) is reduced

• \(K_c\) is increased

• integral control action is introduced

• derivative control action is introduced

GATE-CH-2007-16-ctrl-1mark

An operator was told to control the temperature of a reactor at 60^oC. The operator set the set-point of the temperature controller at 60. The scale actually indicated 0 to 100% of a temperature range of 0 to 200^o C. This caused a runaway reaction by over-pressurizing the vessel, which resulted in injury to the operator. The actual set-point temperature was

• 200^oC

• 60^oC
  

• 120^oC
  

• 100^oC
  

GATE-CH-2011-44-ctrl-2mark

The following diagram shows a CSTR with two control loops. A liquid phase, endothermic reaction is taking place in the CSTR, and the system is initially at steady state. Assume that the changes in physical properties of the system are negligible.

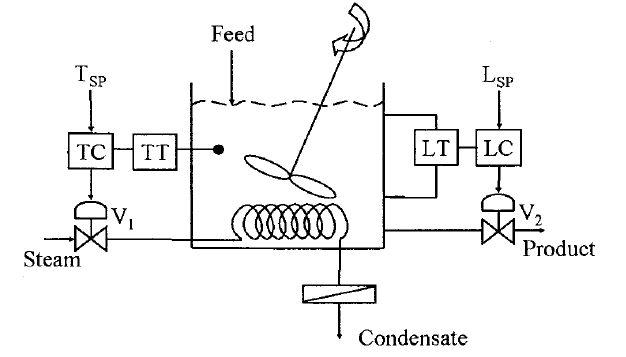
TC: Temperature controller, LC: Level controller, TT: Temperature transmitter, LT: Level transmitter, \(V_1\) and \(V_2\): Control valves. 

Which ONE of the following statements is TRUE?

• Changing the level controller set point affects the opening of \(V_2\) ONLY

• Changing the temperature controller set point affects the opening of \(V_2\) ONLY

• Changing the temperature controller set point affects the opening of BOTH \(V_1\) and \(V_2\)

• Changing the level controller set point affects the opening of BOTH \(V_1\) and \(V_2\)

GATE-CH-2011-8-ctrl-1mark

The range of standard current signal in process instruments is 4 to 20 mA. Which ONE of the following is the correct reason for choosing the minimum signal as 4 mA instead of 0 mA?

• To minimize resistive heating in instruments
• To distinguish between signal failure and minimum signal condition
• To ensure a smaller difference between maximum and minimum signal
• To ensure compatibility with other instruments

GATE-CH-1987-20-i-ctrl-2mark

Determine the (i) sensitivity (in (kN/m\(^2\))/\(^\circ \)C) and (ii) proportional band (in %), of a pneumatic controller with a scale range of 0–120\(^\circ \)C when the output changes from 20–100 kN/m\(^2\) as the temperature rises from 95–110\(^\circ \)C.
(i) sensitivity
{#1}

(ii) proportional band
{#2}

GATE-CH-2006-74-75-ctrl-4mark

The block diagram of a closed loop control system is shown in the figure below. 

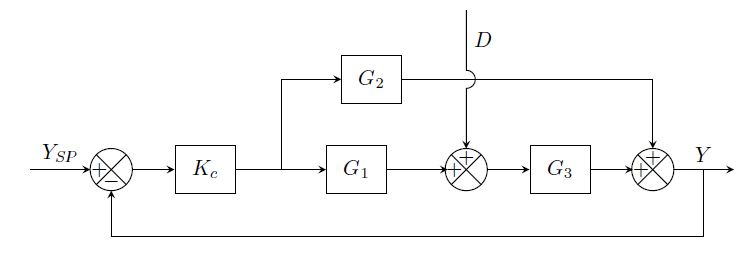
\(Y\) is the controlled variable, \(D\) is the disturbance, \(Y_{SP}\) is the set point, \(G_1, G_2\), and \(G_3\) are transfer functions, and \(K_c\) is the proportional controller.

(i) The closed loop transfer function \(Y(s)/D(s)\) is given by

{#1}

(ii) Let \(G_1(s) = 1\) and \(G_2(s)=G_3(s)=1/(s+1)\). A step change of magnitude \(M\) is made in the set point. The steady state offset of the closed loop response \(Y\) is

{#2}

GATE-CH-2011-54-55-ctrl-4mark

A PID controller output \(p(t)\), in time domain, is given by \[ p(t) = 30 + 5\epsilon (t) + 1.25\int _0^t \epsilon (t) dt + 15\frac {d\epsilon (t)}{dt} \] where \(\epsilon (t)\) is the error at time \(t\). The transfer function of the process to be controlled is \(G_p(s) = \dfrac {10}{200s+1}\). The measurement of the controlled variable is instantaneous and accurate.

(i) The transfer function of the controller is

{#1}

(ii) The characteristic equation of the closed loop is

{#2}

GATE-CH-1998-2-20-ctrl-2mark

A proportional plus integral controller with proportional sensitivity \(K_{c}\) = 1 mA/mA and integral time \(\tau_{I}\) = 1 min is initially at steady state with error signal \(e = 0\) and controller output \(I\) at 10 mA. At time \(t\) = 0, a step change of 1 mA is given in the error signal. The output will show one of the following responses. Identify the correct one.

• \(I\) jumps instantaneously to 11 mA and remains at that value thereafter

• \(I\) increases at a linear rate of 1 mA/min

• \(I\) jumps to 11 mA and then falls exponentially at the rate of \(e^{-t/I}\)

• \(I\) jumps instantaneously to 11 mA and then increases linearly at the rate of 1 mA/min

GATE-CH-1998-2-23-ctrl-2mark

In a closed loop system, the process to be controlled is an integrating process with transfer function \(\dfrac {1}{2s}\). The controller proposed to be used is an integral controller with transfer function \(\dfrac {1}{\tau _Is}\). When a step change in set point is applied to such a closed loop system, the controlled variable will exhibit

• overdamped response

• underdamped response

• undamped response

• unstable response

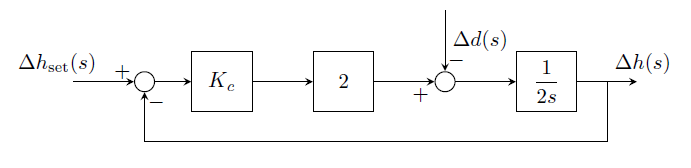
GATE-CH-2001-2-19-ctrl-2mark

The block diagram of an integrating level process is given below. For unit step change in the set point \(\Delta h_{\text{set}} = 1\) with \(\Delta d = 0\), the offset exhibited by the system is

• \(\dfrac{K_c}{1+K_c}\)

• \(\dfrac{1}{1+K_c}\)

• 0

• \(\dfrac{2K_c}{1+2K_c}\)

GATE-CH-2009-43-ctrl-2mark

The block diagram for a control system is shown below:

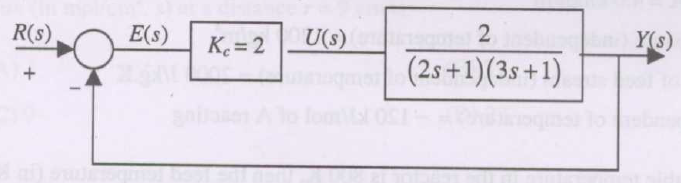
For a unit step change in the set point, \(R(s)\), the steady state offset in the output \(Y(s)\) is

• 0.2

• 0.3

• 0.4

• 0.5

GATE-CH-2010-42-ctrl-2mark

A block diagram for a control system is shown below:

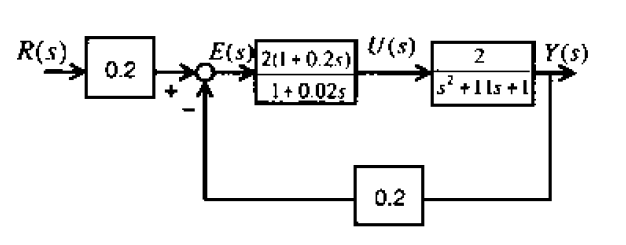
The steady state gain of the closed loop system, between output \(Y(s)\) and setpoint \(R(s)\), is

• 5/9

• 4/9

• 1/3

• 2/9

GATE-CH-1988-18-i-ctrl-4mark

An electronic proportional controller has an input range of 4 to 20 mA and output range of 1 to 5 V. For an input change of 4 mA, what will be the output change (in V), if the proportional band of the controller is 40%.

• Answer

GATE-CH-1988-18-ii-ctrl-4mark

A 5% equal percentage pneumatic valve has an input range 20–100 kN/m\(^2\). When the pressure input is 70 kN/m\(^2\) the corresponding flow rate is 2000 kg/h. If the pressure changes to 80 kN/m\(^2\), what will be the flow rate (in kg/h)?

• Answer

GATE-CH-1994-27-ctrl-5mark

The transfer function of a process, a measuring element and a control valve is given respectively by \[ G_p = \frac {2}{2s + 1}, \quad G_m = \frac {1}{5s + 1}, \quad G_v = \frac {1.5}{3s + 1} \] A proportional controller with a gain of \(K_c = 1\) is used.
Write the closed loop transfer function relating the output (\(Y\)) to the set point (\(Y_r\)).
What is the steady state error in the output for a unit step change in the set point?

• Answer

GATE-CH-1997-8-ctrl-5mark

A control system is shown below.

 
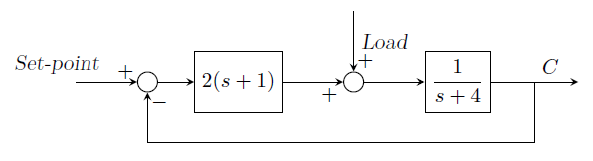
Determine the variation of \(C\) with time for a unit step change in the set-point. What is the offset?

• Answer

GATE-CH-2014-53-ctrl-2mark

Consider the following block diagram for a closed-loop feedback control system:

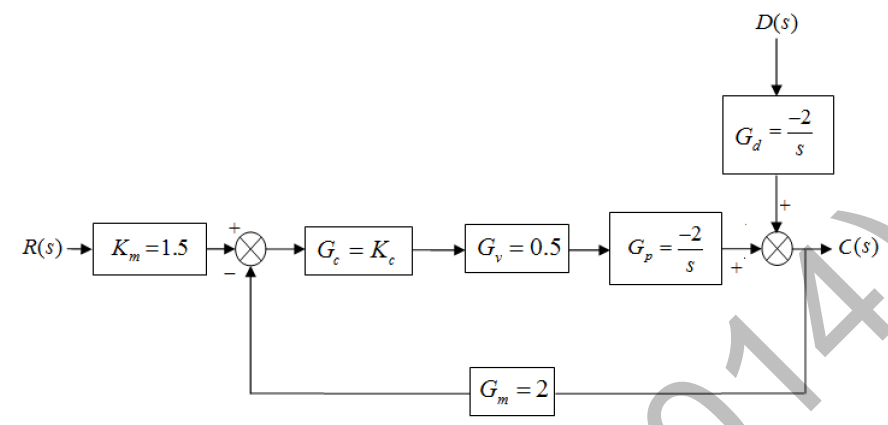
A proportional controller is being used with \(K_c=-4\). If a step change in disturbance of magnitude 2 affects the system, then the value of the offset is ___________

• Answer

GATE-CH-2015-51-ctrl-2mark

The block diagram for a process with feedback control for output deviation variable \(h\) is shown in the figure below. All transfer functions are given with pre-factor of \(s\) in minutes. A unit step change is made in the set-point at \(t=0\). The time required for \(h\) to reach 50% of its ultimate value, in minutes (up to two decimal places), is _____________

• Answer

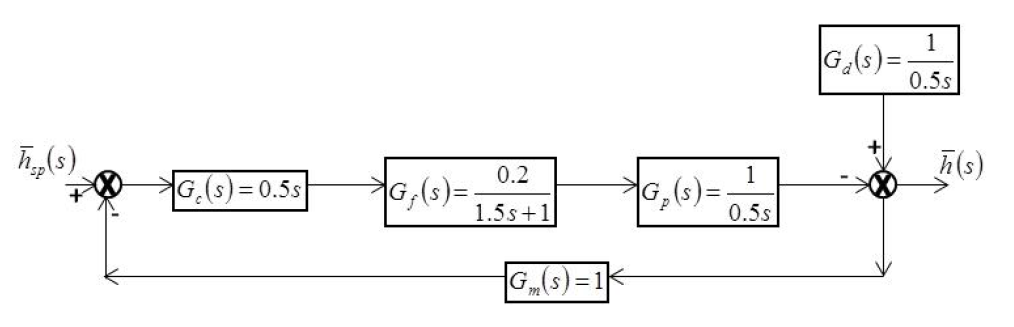
GATE-CH-2018-45-ctrl-2mark

For a closed-loop system, consider the following transfer functions: process \(G_p(s)\), controller \(G_c(s)\), measuring device \(G_m(s)\), and final control element \(G_f(s)\) \[ G_p(s) = \frac{2}{7s+1}; \ G_c(s) = 2; \ G_m(s) = 1; \ G_f(s) = 1 \] The offset in the closed loop response due to a unit step change introduced in the set point of the output variable is ________

• Answer

GATE-CH-1988-18-iii-ctrl-4mark

A control system is represented by the following block diagram:

 
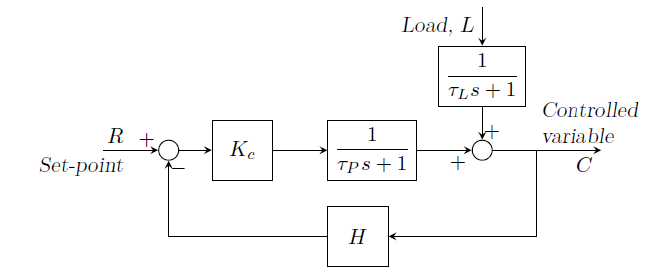
Derive the servo and regulator transfer functions.

• Answer

GATE-CH-2000-15-ctrl-5mark

Given the following block diagram,

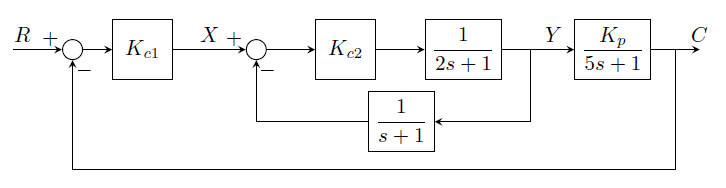
1. Express the transfer function \((Y/X)\) as a ratio of polynomials in \(s\).

2. Calculate the offset in \(C\) due to a unit step change in the reference signal (set-point) \(R\).

• Answer