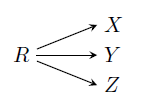Reaction Engineering - GATE-CH Questions
Home -> GATE Questions with Solutions at MSubbu.Academy -> Reaction Engineering->
Multiple Reactions
GATE-CH-1991-8-i-a-cre-2mark
The reaction of \(A\) and \(B\) produces the desired product \(R\) as well as the unwanted product \(S\). What level of reactant concentrations (high, medium, low) should we use for the following reaction scheme in order to maximize the conversion of \(A\) to \(R\).
Reaction scheme: \[ \begin {align*} A + B \rightarrow R \qquad & r_{1} = k_{1}C_{A}C_{B}^{2} \\
A \rightarrow S \qquad \qquad & r_{2} = k_{2}C_{A} \end {align*} \]
GATE-CH-1993-13-b-cre-2mark
For multiple reactions \[ \begin {align*} 2A &\rightarrow R \\
2R &\rightarrow S \end {align*} \] the number of moles of \(S\) present when the number of moles of \(A\) and \(R\) are 0.3 and 0.5 respectively (Initially 2 moles of \(A\) are only present) are
GATE-CH-1994-1-r-cre-1mark
To maximize the formation of \(R\) in the simultaneous reactions \[ \begin {align*} A + B \rightarrow R & r_{R} = 2C_{A}^{0.5}C_{B}^{2} \\
A + B \rightarrow S & r_{S} = 1.4C_{A}C_{B} \end {align*} \] we should have
GATE-CH-2000-1-20-cre-1mark
For the liquid phase parallel reactions
\[ \begin {align*} A &\rightarrow R& r_R &= k_1C_A^2;& E_1 &= 80 \text { kJ/mol} \\
A &\rightarrow S& r_S &= k_2C_A;& E_2 &= 120 \text { kJ/mol} \end {align*} \]
the desired product is \(R\). A higher selectivity of \(R\) will be achieved if the reaction is conducted at
GATE-CH-2003-19-cre-1mark
For a series of reactions \(A \stackrel {k_1}{\longrightarrow } B \stackrel {k_2}{\longrightarrow } C\) having \(k_1 \ll k_2\), the reaction system can be approximated as
[Index]
GATE-CH-2011-22-cre-1mark
Reactant \(R\) forms three products \(X\), \(Y\), and \(Z\) irreversibly, as shown below.
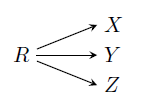
The reaction rates are given by
\(r_X=k_XC_R\),
\(r_Y=k_YC_R^{1.5}\) and
\(r_Z=k_ZC_R\). The activation energies for formation of
\(X\),
\(Y\), and
\(Z\) are 40, 40 and 5 kJ/mol respectively. The pre-exponential factors for all reactions are nearly same. The desired conditions for MAXIMIZING the yield of
\(X\) are
GATE-CH-2012-20-cre-1mark
Consider the reaction scheme shown below \[ A \xrightarrow {k_1} B \xrightarrow {k_2} C \] Both the reactions are first-order. The activation energies for \(k_1\) and \(k_2\) are 80 and 20 kJ/mol, respectively. To maximize the yield of \(B\), it is preferable to use
GATE-CH-2016-15-cre-1mark
The variations of the concentrations (\(C_A\), \(C_R\) and \(C_S\)) for three species (\(A\), \(R\) and \(S\)) with time, in an isothermal homogeneous batch reactor are shown in the figure below.
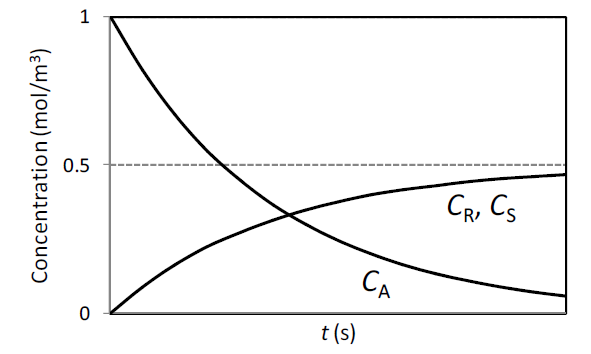
Select the reaction scheme that correctly represents the above plot. The numbers in the reaction schemes shown below, represent the first order rate constants in unit of s
-1.
GATE-CH-1989-17-ii-cre-4mark
Consider the following reaction: \[ \begin {align*} A + B &\stackrel {1}{\longrightarrow } P \text { (desired)} \\
A + B &\stackrel {2}{\longrightarrow } Q \text { (undesired)} \end {align*} \] \(r_1=100\exp (-3000/T)C_AC_B^{0.5}\)
\(r_2=10\exp (-2000/T)C_A^{0.5}C_B\)
The selectivity is defined as the moles of \(P\) produced per mole of \(Q\) produced. In a perfectly mixed tank reactor operated under steady state, in order to maximize the selectivity:
(a) should the inlet concentration of the reactant \(A\) be high or low?
{#1}
(b) should the inlet concentration of the reactant \(B\) be high or low?
{#2}
(c) should the temperature of the reactor be high or low?
{#3}
Explain briefly.
GATE-CH-1999-16-cre-5mark
Two parallel first order reactions \(A \stackrel {k_1}{\longrightarrow } B\) and \(A \stackrel {k_2}{\longrightarrow } C\) are taking place in liquid phase in a well mixed batch reactor. After 60 min of operation, 80% of \(A\) has reacted awhile 2 moles of \(B\) per mole of \(C\) was detected in the reactor. Calculate the rate constants \(k_1\) and \(k_2\) for the two reactions. Assume that no \(B\) and \(C\) were initially present in the reactor.
(i) \(k_1\) = ____________min\(^{-1}\).
{#1}
(ii) \(k_2\) = ____________min\(^{-1}\).
{#2}
[Index]
GATE-CH-2008-71-72-73-cre-6mark
Methane and steam are fed to a reactor in molar ratio 1 : 2. The following reactions take place,
\[ \begin {eqnarray*} \text {CH}_4\text {(g)} + 2\text {H}_2\text {O}\text {(g)} &\rightarrow &\text {CO}_2\text {(g)} + 4\text {H}_2\text {(g)} \\ \text {CH}_4\text {(g)} + \text {H}_2\text {O}\text {(g)} &\rightarrow & \text {CO}\text {(g)} + 3\text {H}_2\text {(g)} \end {eqnarray*} \]
where CO2 is the desired product, CO is the undesired product and H2 is a byproduct. The exit stream has the following composition
| Species |
CH4 |
H2O |
CO2 |
H2 |
CO |
| Mole % |
4.35 |
10.88 |
15.21 |
67.39 |
2.17 |
(i) The selectivity for desired product relative to undesired product is
{#1}
(ii) The fractional yield of CO2 is (where fractional yield is defined as the ratio of moles of the desired product formed to the moles that would have been formed if there were no side reactions and the limiting reactant had reacted completely)
{#2}
(iii) The fractional conversion of methane is
{#3}
GATE-CH-2002-2-13-cre-2mark
In the hydrodealkylation of toluene to benzene, the following reactions occur
\[ \begin {eqnarray*} \text {C}_7\text {H}_8 + \text {H}_2 &\rightarrow & \text {C}_6\text {H}_6 + \text {CH}_4 \\ 2\text {C}_6\text {H}_6 &\rightleftharpoons & \text {C}_{12}\text {H}_{10} + \text {H}_2 \end {eqnarray*} \]
Toluene and hydrogen are fed to a reactor in a molar ratio 1:5. 80% of the toluene gets converted and the selectivity of benzene (defined as moles of benzene formed/ moles of toluene converted) is 90%. The fractional conversion of hydrogen is
GATE-CH-2006-53-cre-2mark
Consider the following elementary reaction network
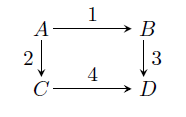
The activation energies for the individual reactions are
\(E_1 = 100\) kJ/mol,
\(E_2 = 150\) kJ/mol,
\(E_3 = 100\) kJ/mol, and
\(E_4 = 200\) kJ/mol. If the feed is pure
\(A\) and the desired product is
\(C\), then the desired temperature profile in a plug flow reactor in the direction of flow should be
GATE-CH-2007-54-cre-2mark
The following liquid phase reaction is taking place in an isothermal CSTR
\[ \begin {eqnarray*} & & A \xrightarrow {k_1} B \xrightarrow {k_2} C \\ & & 2 A \xrightarrow {k_3} D \end {eqnarray*} \]
Reaction mechanism is same as the stoichiometry given above. Given: \(k_1=1\) min-1; \(k_2=1\) min-1; \(k_3=0.5\) litre/(mol.min); \(C_{A0}=10\) mol/litre, \(C_{B0}=0\) mol/litre and \(C_B = 1\) mol/litre, the solution for \(F/V\) (flow rate/reactor volume in min-1) yields
GATE-CH-2007-59-cre-2mark
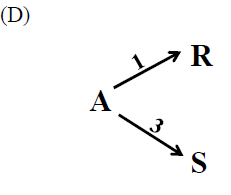
Determine the level of \(C_{A0}\) (high, low, intermediate), temperature profile (high, low, increasing, decreasing), which will favor the formation of the desired product indicated in the reaction scheme given below.
\[\begin{aligned} & A \xrightarrow{1} R \xrightarrow{3} S_{\text{desired}} \\ & A \xrightarrow{2} U\end{aligned}\]
| \(n_1\) |
\(E_1 \qquad\) |
\(n_2\) |
\(E_2 \qquad\) |
\(n_3\) |
\(E_3\) |
| 2 |
25 |
1 |
35 |
3 |
45 |
[Index]
GATE-CH-2008-56-cre-2mark
The elementary liquid phase series parallel reaction scheme
\[ \begin {eqnarray*} & & A \rightarrow B \rightarrow C \\ & & A \rightarrow R \end {eqnarray*} \]
is to be carried out in an isothermal CSTR. The rate laws are given by
\[ \begin {eqnarray*} r_R &=& k’ C_A \\ r_B &=& k C_A - k C_B \end {eqnarray*} \]
Feed is pure \(A\). The space time of the CSTR which results in the maximum exit concentration of \(B\) is given by
GATE-CH-1997-23-cre-5mark
The liquid phase parallel reactions \[\begin {align*} A &\rightarrow R; \qquad r_R = k_1C_A; \qquad k_1 = 0.3 \text { s\(^{-1}\)} \\
A &\rightarrow S; \qquad r_S = k_2; \qquad k_2 = 0.3 \text { kmol/(m\(^3\).s)} \end {align*} \] is conducted in an isothermal plug flow reactor. The inlet concentration of \(A\) is 2.0 kmol/m\(^3\). No products are present in the feed. If conversion of \(A\) is 80%, then determine the exit concentration of \(R\) (in kmol/m\(^3\)).
GATE-CH-1988-7-a-ii-cre-1mark
Consider the reactions \(A\rightarrow B\) and \(A\rightarrow C\), in an isothermal batch reactor. If the orders of the reaction differ, a low concentration of \(A\) favours the reaction of ––––- order.
GATE-CH-1992-18-c-cre-3mark
Consider the set of elementary reactions: \[ \begin {align*} A &\stackrel {k_1}{\rightarrow } B \\
A + B &\stackrel {k_2}{\rightarrow } C \\
A + D &\stackrel {k_3}{\rightarrow } 2E \end {align*} \] At time \(t=0\), a batch reactor is filled with a mixture of \(A\) and \(D\). What is the relation between the concentrations of \(B\) and \(D\) after a time \(t\)?
GATE-CH-2003-71-72-cre-4mark
The following gas phase reactions are carried out isothermally in a CSTR
\( \begin {eqnarray*} A \rightarrow 2 R \quad & & r_1 = k_1P_A \quad k_1 = 20 \text { mol/(s.m$^3$.bar)} \\ A \rightarrow 3 S \quad & & r_2 = k_2P_A \quad k_2 = 40 \text { mol/(s.m$^3$.bar)} \end {eqnarray*} \)
total pressure = 1 bar; \(F_{A0}\) = 1 mol/s; feed is pure \(A\)
(i) What is the maximum possible value of \(F_R\) (mol/s)?
{#1}
(ii) The volume of a CSTR required for a fractional conversion of \(A\) equal to 0.3 due to the first reaction is
{#2}
GATE-CH-2007-74-75-cre-4mark
The following liquid phase reaction is taking place in an isothermal batch reactor \[ A \xrightarrow {k_1 (\text {first order}) } B \xrightarrow {k_2 (\text {zero order}) } C \] Feed concentration = 1 mol/litre.
(i) The time at which the concentration of \(B\) will reach its maximum value is given by
{#1}
(ii) The time at which the concentration of \(B\) will become zero is given by the following equation:
{#2}
GATE-CH-2013-50-51-cre-4mark
Liquid reactant \(A\) decomposes as follows
\[ \begin {align*} A \rightarrow R \qquad r_R &= k_1C_A^2 \qquad k_1 =0.5 \text { m$^3$/mol.s} \\ A \rightarrow S \qquad r_S &= k_2C_A \qquad k_2 = 1 \text { s$^{-1}$} \end {align*} \]
An aqueous feed of composition \(C_{A0} = 30\) mol/m3, \(C_{R0} = 2\) mol/m3, and \(C_{S0}= 1\) mol/m3 enters a CSTR in which the above reactions occur. Assume isothermal and steady state conditions.
(i) If the conversion of \(A\) is 80%, the concentration of \(R\) in the exit stream in mol/m3, to the nearest integer, is ____________
{#1}
(ii) What is the % conversion of \(A\), to the nearest integer, so that the concentration of \(S\) in the exit stream is 11.8 mol/m3? ____________
{#2}
[Index]
Last Modified on: 01-May-2024
Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in