Reaction Engineering - GATE-CH Questions
Home -> GATE Questions with Solutions at MSubbu.Academy -> Reaction Engineering->
Heat Effects
GATE-CH-1990-7-i-cre-2mark
An exothermic gas phase reaction proceeds according to the equation \(3A + 2B \Leftrightarrow 2R\). The equilibrium conversion for this reaction:
GATE-CH-1996-1-1-cre-1mark
The energy balance equation over a tubular reactor under transient conditions is
GATE-CH-1996-2-13-cre-2mark
When an exothermic reversible reaction is conducted adiabatically the rate of reaction
GATE-CH-1997-1-17-cre-1mark
A reversible liquid phase endothermic reaction is to be carried out in a plug flow reactor. For minimum reactor volume, it should be operated such that the temperature along the length
GATE-CH-2002-1-10-cre-1mark
An exothermic reaction takes place in an adiabatic reactor. The product temperature __________ the reactor feed temperature.
[Index]
GATE-CH-2004-24-cre-1mark
An endothermic aqueous phase first order irreversible reaction is carried out in an adiabatic plug flow reactor. The rate of reaction
GATE-CH-1997-22-cre-5mark
The first order, exothermic, irreversible, liquid phase reaction \(A\rightarrow B\) is to be conducted in an adiabatic CSTR. The desired conversion is 70% and the reactor is to be operated at 353 K.
Data:
The rate constant at 353 K = 0.02 s\(^{-1}\)
Inlet volumetric flow rate = 0.01 m\(^3\)/s
Density of the inlet stream = 1000 kg/m\(^3\)
Inlet concentration of \(A\) = 2.0 kmol/m\(^3\)
Heat of reaction (independent of temperature) = \(-50,000\) kJ/kmol of \(A\) reacting
Average heat capacity of inlet and outlet streams = 2 kJ/kg.K
For the data given above, find
(a) the required volume of the CSTR (in m\(^3\)).
{#1}
(b) the feed temperature (in K).
{#2}
GATE-CH-2002-2-6-cre-2mark
A batch adiabatic reactor at an initial temperature of 373 K is being used for the reaction \(A\rightarrow B\). Assume the heat of reaction is \(-1\) kJ/mol at 373 K and the heat capacity of both \(A\) and \(B\) to be constant and equal to 50 J/mol.K. The temperature rise after a conversion of 0.5 will be
GATE-CH-2003-69-cre-2mark
A CSTR is to be designed in which an exothermic liquid phase first order reaction of the type \(A\rightarrow R\) is taking place. The reactor is to be provided with a jacket in which coolant is flowing. Following data is given:
\(C_{A0} = 5\) kmol/m3; \(X_A = 0.5\);
feed temperature = reactor temperature = 40oC;
rate constant at 40oC = 1 min-1;
\(\Delta H = -40\) kJ/mol;
\(\rho = 1000\) kg/m3; \(C_P = 4\) J/g.oC; \(q = 10^{-3}\) m3/min
(\(\rho \) and \(C_P\) are same for the reactant and product streams).
The amount of heat to be removed is
GATE-CH-2004-77-cre-2mark
An irreversible aqueous phase reaction \(A + B \rightarrow P\) is carried out in an adiabatic mixed flow reactor. A feed containing 4 kmol/m3 of each \(A\) and \(B\) enters the reactor at 8 m3/h. If the temperature of the exit stream is never to exceed 390 K, what is the maximum feed inlet temperature allowed?
Data :
Heat of reaction = \(-50\) kJ/mol,
density of the reacting mixture = 1000 kg/m3,
specific heat of reacting mixture 2 kJ/kg K.
The above data can be assumed to be independent of composition and temperature.
[Index]
GATE-CH-2006-34-cre-2mark
Pure \(A\) at 200oC is fed to a steady state adiabatic continuous reactor at the rate of 100 kg/hr where it undergoes an exothermic reaction to give its isomer \(B\). The product stream is at temperature 500oC. The heat of reaction is 21 kJ/mol of \(A\) and the specific heat of the reaction mixture is constant at 35 J/(mol.oC). The conversion in the reactor is
GATE-CH-2008-58-cre-2mark
The homogeneous reaction \(A + B \rightarrow C\) is conducted in an adiabatic CSTR at 800 K so as to achieve a 30\% conversion of \(A\). The relevant specific heats and enthalpy change of reaction are given by:
\(C_{P,A} = 100\) J/(mol.K), \(C_{P,C} = 150\) J/(mol.K)
\(C_{P,B} = 50\) J/(mol.K), \(\Delta H_{\text {rxn}} = -100\) kJ/mol
If the feed, a mixture of \(A\) and \(B\), is available at 550 K, the mole fraction of \(A\) in the feed that is consistent with the above data is
GATE-CH-2012-41-cre-2mark
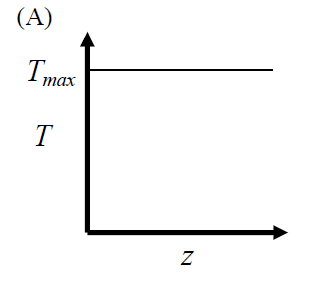
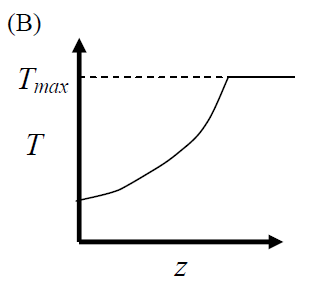
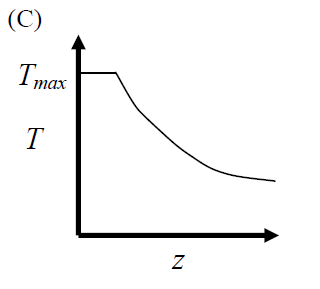
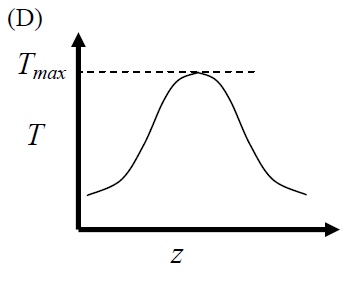
The elementary reversible exothermic gas-phase reaction \[ A + 3B \rightleftharpoons 2C \] is to be conducted in a non-isothermal plug flow reactor. The maximum allowable reactor temperature is \(T_{\text {max}}\). To minimize the total reactor volume, the variation of reactor temperature (\(T\)) with axial distance from the inlet (\(z\)) should be
GATE-CH-1991-18-i-cre-6mark
For a reversible exothermic elementary catalytic reaction of the type \( \ce {A <=>[k_1][k_2] R} \) find the optimum operating reaction temperature at a conversion level \(X_A = 0.8\).
Data: \[ \begin {align*} k_1 &= \exp (10-5000/T) \\
k_2 &= \exp (40-15000/T) \end {align*} \] Maximum allowable temperature = 300 K.
____________
GATE-CH-2016-48-cre-2mark
A liquid phase irreversible reaction \(A\rightarrow B\) is carried out in an adiabatic CSTR operating under steady state conditions. The reaction is elementary and follows the first order rate law. For this reaction, the figure below shows the conversion (\(X_A\)) of \(A\) as a function of temperature (\(T\)) for different values of the rate of reaction (\(-r_A\) in mol.m\(^{-3}\).s-1) denoted by the numbers to the left of each curve. This figure can be used to determine the rate of the reaction at a particular temperature, for a given conversion of \(A\).
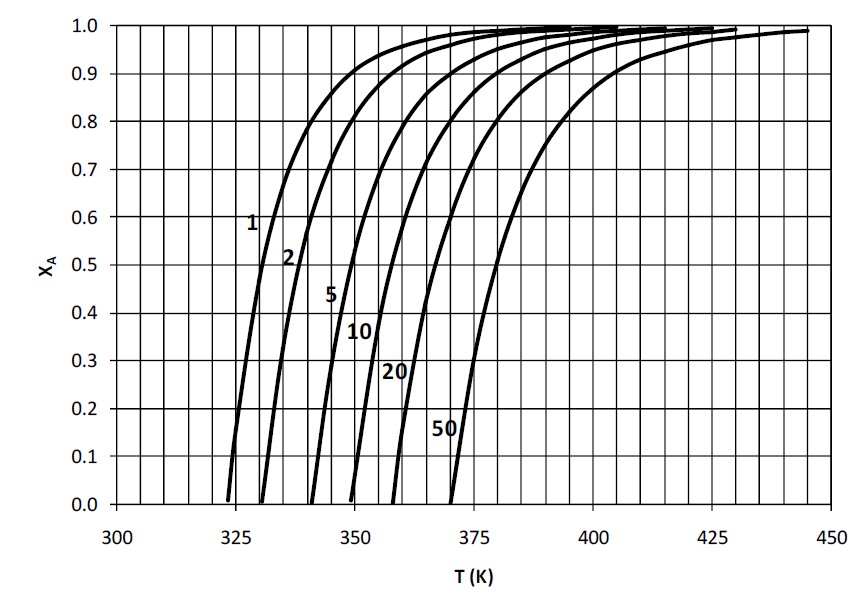
The inlet stream does not contain
\(B\) and the concentration of
\(A\) in the inlet stream is 5 mol/m
3. The molar feed rate of
\(A\) is 100 mol/s. A steady state energy balance for this CSTR results in the following relation:
\(T=350+25X_A\) where
\(T\) is the temperature (in K) of the exit stream and
\(X_A\) is the conversion of
\(A\) in the CSTR. For an exit conversion of 80% of
\(A\), the volume (in m
3, rounded off to the first decimal place) of CSTR required is ____________
GATE-CH-2017-31-cre-2mark
Reaction \(A\rightarrow B\) is carried out in a reactor operating at steady state and 1 mol/s of pure \(A\) at 425oC enters the reactor. The outlet stream leaves the reactor at 325oC. The heat input to the reactor is 17 kW. The heat of reaction at the reference temperature of 25oC is 30 kJ/mol. The specific heat capacities (in kJ/mol.K) of \(A\) and \(B\) are 0.1 and 0.15, respectively.
The molar flowrate of \(B\) leaving the reactor, rounded to 2 decimal places, is ____________mol/s.
GATE-CH-1999-18-cre-5mark
For an exothermic reaction \(A\rightarrow B\), 90 kmol of \(B\) are to be produced while achieving 90% conversion of \(A\) in an isothermal batch reactor operated at 500 K. The reaction is to be started with pure \(A\) at the concentration of 10 kmol/m\(^3\). Determine the volume of the reactor, duration of the batch operation and the total heat removed during the isothermal operation. The heat of the reaction at 500 K is \(-40\) kJ/mol of \(A\) reacted. Following additional information is available to determine the order and rate constant of the reaction. Laboratory experiments conducted at 500 K with 1 kmol/m\(^3\) initial concentration of pure \(A\) showed that 20% conversion is obtained in 20 min, while 50% conversion is obtained in 80 min. The reaction is suspected to be either first or second order.
(i) order of reaction (1 or 2)
{#1}
(ii) rate constant of reaction
____________\(\times 10^{-5}\text { m}^3/\text {(mol.min)}\)
{#2}
(iii) volume of reactor (m\(^3\))
{#3}
(iv) duration of batch operation (min)
{#4}
(v) heat removed (MJ)
{#5}
GATE-CH-1996-5-cre-5mark
At a given space time \(\tau \), a mixed reactor is operated at a temperature which maximizes the concentration \(C_R\) of the desired product for the elementary reactions \[ A \stackrel {k_1}{\longrightarrow } R \stackrel {k_2}{\longrightarrow } S \] \(k_1\) = 0.0333 s\(^{-1}\), \(\tau \) = 300 s, \(E_1/E_2\) = 3, where \(E_1\) and \(E_2\) are the activation energies of the two reactions. Find the value of \(k_2\) at this temperature. The feed to the reactor consists of pure \(A\).
\(k_2\) = ____________\(\times 10^{-3} \text { s}^{-1}\)
[Index]
Last Modified on: 01-May-2024
Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in